چند فرمول ریاضی بسیار عجیب و غریب

ریاضی در نگاه اول علمی خشک و تنها برپایه قوانین منطقی به نظر می رسد اما دانشمندان در سال گذشته اثبات کردند که این علم از مهارت بالایی برای سرگرم کردن مردم و دلچسب کردن زندگی روزمره برخوردار است

فرمول ریاضی تهیه یک فنجان چای مطبوع!

چای یکی از بهترین نوشیدنیها است. ممکن است بسیاری از مردم تصور کنند که تهیه یک چای عالی هنر است. در سالی که گذشت گروهی از دانشمندان دانشگاه اومبریای شمالی در انگلیس نشان دادند که تهیه یک چای خوب بیش از آنکه هنر باشد، علم است.

این دانشمندان با ارائه یک فرمول ریاضی راز تهیه یک فنجان چای مطبوع را نشان دادند. برپایه این فرمول ریاضی، دمای مطلوب برای نوشیدن چای 60 درجه سانتیگراد است که 6 دقیقه پس از ریختن این نوشیدنی در فنجان به دست می آید. اما پس از گذشت 17 دقیقه و 30 ثانیه، دمای چای به 54 درجه سانتیگراد می رسد که بهترین دما برای لذت بردن از آن است.

فرمول ریاضی یک فنجان چای مطبوع:

TB+ (H2O) 2mins BT+ C(10 ml) 6 mins BT= PC(OT 60°c

توضیح علائم اختصاری:

TB یک چای کیسه ای

BT زمان دم کردن/ در این فرمول دو دقیقه

 H2O آب

C شیر/ در این فرمول 10 میلی لیتر

PC یک فنجان چای مطبوع

OT دمای مناسب برای نوشیدن چای/ در این فرمول 60 درجه سانتیگراد

افراد متولد هر ماه در آینده چه شغلی پیدا می کنند

دانشمندان علم نجوم بارها تائید کرده اند که طالع بینی از روی حرکت ستارگان و کواکب و یا کف بینی ریشه علمی ندارد. شاید به همین منظور پژوهشگران اداره ملی آمار انگلیس در یک تحقیق کاملاً جدی و با استفاده از اطلاعات تازه ترین سرشماری ماههای تولد افرادی را که در 19 شغل مختلف مشغول به کار هستند، تجزیه و تحلیل کرده و نوع ارتباط میان ماه تولد و شغل آینده را تعیین کردند. هرچند ذکر این نکته ضروری است که این طالع بینی تنها براساس اطلاعات آماری و تنها در انگلیس انجام شده اند و بنابراین به نظر می رسد که همانند سایر طالع بینی ها معتبر نیست.

برپایه این بررسیها برای مثال بیشتر دندانپزشکان متولد ماه دسامبر هستند درحالی که ماه فوریه برای پرورش هنرمندان ماه ایده آلی است. تعداد پزشکان عمومی و ماموران مالیات در ماه ژانویه افزایش می یابد.

منبع:ferz.ir

ابزاري مناسب براي رسم نمودار توابع وانواع تبديلات

powerToy Calculator ابزاري مناسب براي رسم نمودار توابع وانواع تبديلات
اين نرم افزار به پيچيدگي نرم افزارهاي پيشرفته اي مثل MATLAB , MAPLE و... نيست و در عين حال ابزار قدرتمندي براي رسم انواع نمودارها و تبديلات و يك ماشين حساب قدرتمند است اين نرم افزار را مي توانيد از لينك زير دانلود كنيدلینک دانلود

توجه داشته باشيد از لينك داده شده روي دكمه free كليك كنيد

دنباله فیبوناتچی وچند تابع ریاضی به روش بازگشتی به زبان c

فیبوناتچی:

include
int fib(int n);
main()
{
int n;
printf("enter number");
scanf("%d",&n);
printf("%d",fib(n));
getch();
}
int fib(int n)
{
if(n==1 ||n==2)
return(1);
else
return(fib(n-1)+fib(n-2));
}

---------------------------------------------------------------------------------------------------------------------------------------
فاکتوریل:

include
include
int fact(int);
main()
{
int i,n;printf("enter number to calcute factorial");
scanf("%d",&n);
    for(i=1;i<=n;i++)
    printf("%d",fact(i));
    getch();
 {
int fact(int i)
{
  int n;
   if(n!=0)
    return(n*fact(n-1));
    return(1);
 }
------------------------------------------------------------------------------------------------------------------------------------------

xبه قوه :y

include

include

double dpower(long double x,int y);
main()
{
double x,y;
printf("enter to namber to calcute power");
sacnf("%d %d",&x,&y);
printf("%d",dpower(x,y));
getch();
}
double dpower(double x,int y)
{
if (y==1)
   return(x);
 else
     return (x*dpower(x,y-1));
}

نکته:علامت # در اول include فراموش نشود

ریاضی و موبایل(نرم افزار)

 

در دنیای امروز که عصر ارتباطات است داشتن یک موبایل یک امر ضروری الزامی است .در گذشته

 

کاربردهای موبایل فقط در برقراری ارتباط تلفنی یا اس ام اس خلاصه می شد ولی امروزه موبایل تنها وسیله

 

تماس نیست; بلکه مینی کامپیوتر است که با آن می توان ایمیل چک کرد،موسیقی گوش داد و فایل به

 

اشتراک گذاشت .

 

سیستم عامل موبایلها انواع مختلفی دارد از جمله Windows mobile، simbian و... که اینها قابلیت

 

اجرای نرم افزارهای مختلف را دارند برای یک دانشجوی ریاضی داشتن نرم افزاری که بتواند تبدیل واحدها

 

،محاسبات مثلثاتی ، معادلهای ریاضی بر حسب نمودار را انجام دهد امری الزامی است در اینجا ما با معرفی

 

چندین سایت که این نرم افزارها را در اختیار شما قرار می دهد معرفی می کنیم لازم به ذکر است بیشتر

 

فایلها با پسوند sisاست و روی پلت فرم simbians s60اجرا می شوند .

 

این سایتها عبارتند از :          www.mobile9.ir    -  www.mobile9.com

 

در ضمن از عبارات کلیدی: free software for mobile ، mobile math  نیز در جستجوگر Google

 

یاهر جستجو گر دیگری نیز می توانید لینک دانلود کنید.

 دانلود

حدس گلدباخ

حدس اولیه گلدباخ ابتدا در ۷ ژوئن ۱۷۴۲ نامه او به اویلر اینگونه بیان شد:”به نظر می رسد هر عدد بزرگتر از ۲ را می توان به صورت جمع سه عدد نوشت.”
باید متذکر شد که در این جمله گلدباخ یک را عدد اول فرض نمود. اویلر شرح دیگری از حدس را بیان کرد که در واقع معادل با حدس اولیه بود. او ادعا نمود هر عدد زوج بزرگتر از ۴ را می توان به صورت جمع دو عدد اول نوشت.
دو عدد اول (P,q) که P+q=۲n و n عددی صحیح و مثبت باشد را معمولا افراز گلدباخ می نامند. در سال ۱۹۷۷ پوگوزلسکی مدعی اثبات حدس گلدباخ شد اما اثبات او به طور کلی پذیرفته نشد.
همچنین حدس “هر عدد فرد بزرگتر از ۹ جمع سه عدد اول فرد است” را حدس ضعیف گلدباخ می نامند. وینوگرادف ثابت کرد هر عدد فرد به اندازه کافی بزرگ جمع سه عدد اول است
منبع: مسائل حل نشده در نظریه اعداد،

نرم افزار فراکتال

«هندسه فراکتال» شاخه ای از علم ریاضیات است که در اوایل قرن 19 میلادی مورد توجه ریاضیدانان قرار گرفت.فراکتالها الگوهای هندسی (مربع ، دایره و...) هستند که در اندازه های کوچک و بزرگ بر روی یک صفحه و یا فضا قرار دارند و مرتبا تکرار می شوند.شکلهای موجد در هندسه کلاسیک یا همان «هندسه اقلیدسی»، می توانند صفر بعدی مانند نقطه،1 بعدی مانند خط ، دو بعدی مانند مربع ،و سه بعدی مانند یک مکعب باشند .اما در طبیعت ، شکلها و رفتارهایی را می توان یافت که قابل توصیف توسط هندسه کلاسیک نیستند (مانند گسلها و یا خط سیر یک زمین لرزه).این رفتارها و شکلها ،توسط «هندسه فراکتال» قابل توجیه و توصیف هستند.
Fractal Explorer
نرم افزارهای متعددی برای تولید تصاویر فراکتال وجود دارند،اما نکارنده در اینجا برنامه Fractal Explorer را انتخاب کرده ام .ایت برنامه قادر است فراکتالهای نوع 1و2 را تولید کند،اما ما در این جا فقط به نوع اول یعنی Complex Number می پردازیم .توضیح دیگر اینکه این برنامه به طور کامل توسط Delphi نوشته شده است، و معمولا اینگونه برنامه ها به علت خصوصیات ویژه خود ،توسط Visual Basic و Delphi نوشته می شوند.البته برنامه های دیگری از این نوع نیز وجود دارند که به زبانهای همچون Java و حتی C++ نوشته شده اند ، ولی تعداد آنها انگشت شماراست .خب ، به بحث اصلی خود برسیم.
در این مبحث فرض شده است که شما کاربر گرامی ، آشنایی کافی با ذخیره کردن و باز کردن فایلهای پروژه برنامه دارید.همچنین شما می توانید نسخه کامل برنامه Fractal Explorer را از آدرس
http://www.eclectasy.com/Fractal-Explorer/download.htm بارگزاری کنید.در اینجا ذکر چند نکته واجب است .بعد از اینکه به آدرس فوق رفتید،سه قسمت Fractal Explorer و Fractal Landscapes Library و User Formula Compiler برای بارگزاری موجود می باشند.شما بتدا فایل Fractal Explorer را بارگزاری کرده و در جایی از هارد دیسک خود قرار دهید.سپس فایلهای Fractal Landscapes Library و User Formula Compiler را بارگزاری کرده و آنها رادر همان جایی که برنامه اصلی قرار دارد ،کپی کنید.این برنامه نیازی به نصب کردن ندارد و برای اجرای آن فقط بر روی آیکون آن که مطابق شکل یک فراکتال است ، دوبار کلیک کنید.

نقش اروپا در پیشرفت ریاضیات

یکی از ریاضیدانان قرن سیزدهم میلادی در اروپا لئونارد بوناکسی( 1170-1220 م. ) ریاضیدان ایتالیایی است. وی که مدتها در مشرق زمین اقامت کرده بود، آثار برخی از دانشمندان اسلامی را از آنجا به ارمغان آورد. وی برای اولین بار در اروپا علم جبر را در هندسه مورد استفاده قرار داد. در قرن پانزدهم و در قرن شانزدهم دانشمندان ایتالیایی ها در حساب عدد ، جبر و مکانیک ترقیات شایان کردند.
در اواخر قرن شانزدهم در فرانسه دانشمندی به نام فرانسوااویت ( 1540-1603م.) به پیشرفت علوم ریاضی خدمات ارزنده ای نمود.مثلثات جدید نیز حاصل زحمات اوست. او نخستین ریاضیدانی بود که برای حل مسئله ترسیم دایره ای مماس بر سه دایره دیگر راه حل هندسی بدست آورد و ریشه های معادله درجه چهارم را ساخت.
ریاضیـدانان کشـور هلنـد نیز در پیشـرفت و رشد دانش ریاضی بسیـار مؤثر بودند.آدرین رومن و سپس آدرین متیوس مقدار تقریبی عدد پی را محاسبه کردند و یکی دیگر از هموطنان آنان به نام وان سولن تا 35 رقم اعشاری آن را بدست آورد.
کشف لگاریتم یکی از پیشرفتهای بسیار مهم در تاریخ علم ریاضیات است. کاشف آن جان نپر یا ناپیه ( 1556-1317 م. ) ریاضیدان معروف اسکاتلندی است. یکی از آثار او کتاب معروف لگاریتمی است که در سال 1614 م. تألیف کرد.
نپر نخستین دانشمندی بود که محاسبه اعشار را جانشین محاسبات کسری معمولی نمود.عصای نپر ،اسبابی بوده که برای تسهیل اعمال ریاضی که عمل ضرب را جانشین جمع و عمل تقسیم را جانشین تفریق ساخته است. نظیر خط کش محاسبه که امروزه مورد استفاده مهندسین است.
یکی دیگر از نوابغ علم ریاضی در قرن هفدهم بلز پاسکال( 1623-1662 م. ) است که در پیشرفت حساب دیفرانسیل بسیار مؤثر بود،وی در 18 سالگی ماشین محاسبه را اختراع کرد.
باید به کوششهای کپرنیک، کپلر،تیکوبراهه و گالیله و نقش آنان در رشد علم ریاضی نیز اشاره ای کنیم.قرن هفدهم میلادی شاهد ریاضیدانان بزرگی نظیر رنه دکارت ( 1596-1650م. ) فیلسوف و ریاضیدان فرانسوی بود.پیردوفرما ( 1601-1665م. ) ریاضیدان فرانسوی نیز در تحول علم ریاضی در قرن هفدهم بسیار مؤثر بود. وی ظاهراً پیش از دکارت اصول هندسه تحلیلی را اختراع کرد.
وی را مؤسس نظریه مدرن اعداد ( حساب عالی ) و نظریه احتمالات می دانند.در سال 1781 در کشور فرانسه سیمون دنیس پواسون (1781-1840م.) تولد یافت که از ریاضیدانان بزرگ قرن هیجدهم است.
او در سال 1801 آنچنان در ریاضی پیشرفت کرد که به عنوان استاد تجزیه و تحلیل ریاضیات در دانشگاه پاریس برگزیده شد.وی مقالاتی مربوط به مکانیک (1811م. )، یادداشتهایی راجع به تئوری امواج (1826م. )، تئوری ریاضیات در رابطه با حرارت (1835م. ) و تئوری محاسبه احتمالات ( 1838م.) را منتشر ساخت.
لوئی پوانو(1777-1859م.) نیز از ریاضیدانان برجسته قرن نوزدهم است.در نیمـة قـرن نوزدهـم کشـف جورج گرین (1793-1841م. ) ریاضیــدان انگلیسی و شارل فردریک کائوس یا گاوس (1777-1855م.) ریاضیدان آلمانی توجة بسیاری از دانشمندان را جلب کرد.
یکی دیگر از ریاضیدانان بزرگ در قرن نوزدهم اوگوستن لوئی کوشی(1789-1857م.) فرانسوی است که در همه رشته های ریاضیات محض و کاربردی اکتشافاتی داشت، ولی خدمت بزرگ وی آن بود که آنالیز ریاضی را بر مبانی محکم استوار ساخت.کوشی ریاضیات – مخصوصاً آنالیز- را نسبت به قرن هیجدهم سخت دگرگون ساخت.
ویلیام راون هامیلتون (1805-1865م. ) ایرلندی بدون تردید یکی از نوابغ قرن نوزدهم بود.نبوغ و استعداد شگفت او از دوران کودکی اش معلوم شد. او حتی در 5 سالگی متون لاتینی و یونانی و عبری را می خواند و ایتالیایی و فرانسوی را در 8 سالگی و عربی و سانسکریت را در 10 سالگی آموخت و در 14 سالگی برای سفیر ایران خطابه خوشامدی به زبان فارسی تهیه کرد.
این استعداد بی مانند به زودی متوجة علوم گردید، بطوری که در 17 سالگی تمام حساب انتگرال را به خوبی می دانست و خسوف و کسوف را به خوبی پیش بینی می کرد و در 22 سالگی استاد نجوم گردید.
تاریخ ریاضیات گذشته از وقایع شیرین ، وقایع مصیبت بار را نیز ثبت کرده است. داستان گم شدن کشف بزرگ نیل هنریک آبل (1802-1829م.) ریاضیدان جوان و نابغه نروژی یکی از آنهاست. آپل که از نبوغی شگفت انگیز برخوردار بود در 22 سالگی ثابت نمود که صرف نظر از معادلات درجه اول تا درجه چهارم، هیچ دستور جبری که بتواند معادله درجه پنجم را به نتیجه برساند وجود ندارد .
آبل مقاله ای درباره خاصیت عمومی طبقه بسیار وسیعی از توابع غیر جبری انتشار داد.
آبل در این مقاله با ذکر کامل تمام فرمولها که پس از رنج بسیار فراهم کرده بود انتگرالهای بیضوی معروف به انتگرالهای لژاندر را مورد مطالعه قرار داده و مطالب جدیدی را کشف کرده بود که به راستی ارزش بسیار داشت. آبل کشف ذیقیمت خود را به کوشی سپرد، اما کوشی آن را گم کرد.

ادامه بزودی در وبلاگ قرار میگیرد.

تحولات تاریخی دانش مثلثات

مقدمه
واژه "مثلثات" از "مثلث" آمده است و ترجمه‌ای است از واژه فرانسوی هم ارز که به معنای "اندازه گیری مثلث" است. در زبان فارسی، به جای "مثلثات" از واژه "سه بروارگان" استفاده کرده‌اند. از نامگذاری "مثلثات" می‌توان حدس زد که، این شاخه از ریاضیدانان، برای رفع دشواریهای مربو به محاسباتی دانست که، در هندسه و در اخترشناسی، روبه روی دانشمندان بوده است. در ضمن، دشواریهای هندی خود ناشی از مسائلی بوده است که در اخترشناسی با آن روبرو می‌شده‌اند و بیشتر جنبه محاسبه‌ای داشته‌اند.
مکان یابی نجومی
در اخترشناسی ، برای تعیین جا و موقعیت ستارگان ، فاصله‌های آنها از یکدیگر و این ویژگیهای آنها ، به عدد نیاز داشتند، ولی در راه حل هندسی ، پاسخ را از جمله به صورت یک پاره خط راست به ما می‌دهد و ، در نتیجه کار اخترشناسان را دشوار می‌کرد. کهنترین جدولی که به ما رسیده و در آن طول وترهای برخی کمانهای داده شده است، متعلق به هیپارک اخترشناس سده دوم میلادی است. و شاید بتوان ، تنظیم آن جدول را ، گام نخستین کوچکی ، در راه پیدایش مثلثات دانست. منه لائوس ریاضیدان و بطلیموس اخترشناس در این زمینه ، نوشته‌هایی از خود باقی گذاشته‌اند. ولی همه کارهای ریاضیدانان و اخترشناسان یونانی ، درون هندسه انجام گرفت و هرگز به مفاهیم اصلی مثلثات نرسیدند.

نخستین گام بوسیله آریابهاتا ، ریاضیدان هندی سده اول نجم میلادی برداشته شد که در واقع تعریفی برای نیم وتر یک کمان (یعنی ، همان سینوس) ارائه کرد. از این به بعد ، تقریبا همه کارهای مربوط به شکل گیری مثلثات به ویله دانشمندان ایرانی انجام گرفت، خوارزمی نخستین جدولهای سینوس را تنظیم کرد، و پس از او همه ریاضیدانان ارانی گامهایی برای تکمیل این جدولها و گسترش مفاهیم مثلثاتی برداشتند.
دستاوردهای ایرانیان
کروزی جدول سینوسها را 30 دقیقه به 30 دقیقه تنظیم کرد و برای نخستین بار ، به دلیل نیازهای اخترشناسی ، مفهوم تانژانت را (که ظلل می‌نامیدند) تعریف کرد، جدیترین تلاشها بوسیله ابوریحان بیرونی و ابوالوفای بوزجانی انجام گرفت که توانستند پیچیده‌ترین دستورهای مثلثاتی را پیدا کنند و جدولهای سینوسی - تانژانتی را با دقت بیشتری تنظیم کنند.

سرانجام ، خواجه نصیرالدین طوسی با جمع بندی کارهای دانشمندان ایرانی پیش از خود ، نخستین کتاب مستقل مثلثات را نوشت. بعد از طوسی ، جمشید کاشانی ، ریاضیدان ایرانی زمان تیموریان، با روش زیبایی که برای حل معادله درجه دوم پیدا کرده بود، توانست راهی برای محاسبه سینوس کمان یک درجه و با هر دقت دلخواه پیدا کند. پیشرفت بعدی دانش مثلثات ، از سده پانزدهم میلادی و در اروپای غربی انجام گرفت.
مباحث مرتبط با عنوان(کلمه های کلیدی جستجو)

* تحولات تاریخی دانش ریاضی
* تاریخچه ریاضیات
* تاریخ علم
* حساب دیفرانسیل و انتگرال
* دانشمندان ریاضی
* ریاضیات
* زیباشناسی در ریاضیات
* مثلثات
* هندسه اقلیدسی
* هندسه تحلیلی

ماشین حساب قدرتمند برای windows

 

 

ماشین حساب ویندوز با وجود مفید بودن بسیار و تمامی تواناییهای مختلف به عنوان یک ماشین حساب قدرتمند تخصصی و مهندسی نمی تواند مورد استفاده قرار گیرد.بنابراین وجود یک ماشین حساب قدرتمند وحرفه ای برای تمامی افراد نیازی ضروری است.در این رابطه Deskcalc نام ماشین قدرتمند از شرکت Pmasof است که توسط ان شما قادر به انجام محاسبات خود به آسانی در محیط ویندوز می باشید. صفحه نمایش واضح و قابل تغییر،نمایش راه حل برای شما ،توانایی load وsave ،ویژگی خروجی با فرمت EXEL ومجهز به بخشی برای تبدیل واحدهای گوناگون .
بخشی از ویژگیهای ان است نسخه کامل این نرم افزار ورژن 4،0 و3 با حجم محدود 1.4 مگابایت را از آدرس زیر دریافت کنید.
www.Pmasott.com

خلاصه ای از تاریخچه ریاضی و ریاضیدانان(ریاضیات در قرن ۱۸ میلادی )

۸. ریاضیات در قرن ۱۸ میلادی

---

این قرن را می توان قرن بهره برداری از حسابان نامید. وسیله ای که بلافاصله پس از کشف، قادر به حل مسائلی شد که قبل از آن تسخیر ناپذیر می نمودند. گستردگی کاربرهای آن حتی در مکانیک و نجوم، چنان اعجاب آور بود که اکثر ریاضیدانان این قرن را به خود جذب کرد و باعث تالیف مقالات بسیار شد. متاسفانه دقت کافی نیز در اثبات قضایا منظور نمی شد و کم کم دومین بحران بزرگ تاریخ ریاضیات شکل گرفت (اولین بحران، کشف عدد اصم  در یونان باستان بود). این بحران، ورود بعضی از تناقضات عجیب و غریب در ریاضیات بود. مشکلی که بخش بزرگی از فعالیتهای ریاضیدانان قرن نوزدهم، معطوف به حل آن شد. قرن هجدهم شاهد رشد بیش از پیش نظریه احتمال، معادلات دیفرانسیل، هندسه تحلیلی، نظریه اعداد و نظریه معادلات بود. ضمنا در این قرن معادلات دیفرانسیل با مشتقات جزئی، هندسه ترکیبی و هندسه دیفرانسیل نیز پا به عرصه وجود گذاشتند. حال مشابه روشی که در قرن هفدهم پی گرفتیم به معرفی ریاضیدانان بزرگ این قرن می پردازیم؛ با توجه به این نکته که مطالب زیر بسیار کوتاه و کاملا گزینشی هستند. ذکر این نکته نیز لازم است که برای فهم بعضی از مطالب زیر به معلومات دانشگاهی نیازمندیم.

1.      خانواده برنولی: این خانواده سوئیسی، یکی از متشخص ترین خانواده ها در تاریخ ریاضیات بود. سابقه خانوادگی آنها با دوبرادر، یاکوب برنولی و یوهان برنولی آغاز می شود و با پسران یوهان به نامهای نیکولاس، دانیل و یوهان II و نیز پسر یوهان II، یوهان III و نوادگان دیگر ادامه می یابد. سابقه خانوادگی آنها را می توان از سال ۱۶۵۴ تا ۱۸۶۳ (حدود ۲۱۰ سال) پی گرفت. به جهت اختصار فقط به کارهای دو برادر اول می پردازیم.

- یاکوب برنولی: او کاربردهای مهمی از مختصات قطبی را ارائه نمود، فرمول شعاع انحنای یک منحنی در مختصات دکارتی و قطبی را استخراج کرد، منحنی همزمان را کشف کرد (این منحنی یک سهمی از درجه سه دوم است که مماس در نقطه بازگشت آن قائم است و هر جسم در امتداد آن با سرعت عمودی یکنواختی سقوط میکند)، مساله شکلهای هم پیرامون را طرح نمود
(مسیرهای مسطح بسته ای از انواع مفروض که محیط آنها ثابت و مساحت آنها ماکزیمم است) و کتاب معروف فن حدس زدن را در موضوع احتمال ریاضی تالیف کرد. نام او در ریاضیات با توزیع برنولی و قضیه برنولی در آمار و احتمال، معادله برنولی در معادلات دیفرانسیل، اعداد و چند جمله ایهای برنولی در نظریه اعداد و لمینسکات برنولی در حساب دیفرانسیل و انتگرال همراه است. جالب است که بدانیم که کلمه انتگرال را نیز برای اولین بار، یاکوب برنولی به کار برد.
 
- یوهان برنولی: او به حسابان غنای زیادی بخشید و در شناساندن قدرت آن در اروپا بسیار موثر بود. مقالات متعدد یوهان برنولی را مارکی دو لوپیتال در قالب اولین کتاب درسی حسابان گردآوری و منتشر کرد (بد نیست بدانیم که بعدها قاعده صورت مبهم صفر تقسیم بر صفر به غلط قاعده هوپیتال نام گرفت). محاسبه طول قوس منحنی ها، حسابان توابع توانی و تلاش برای حل دو مساله مهم کوتاهترین زمان و همزمانی که به دست آوردن منحنی هایی با شرایط خاص است، فهرستی از کارهای مهم اوست. ضمنا او یکی از موفقترین معلمین زمان خود بود.

2.      دموآور: آبراهام دموآور یکی از دوستان صمیمی نیوتن بود و با تالیف سه کتاب، نقش مهمی در نظریه آمار و احتمال دارد. بررسی انتگرال احتمالاتی معروف
 

 
برای اولین بار، بررسی منحنی فراوانی نرمال   که c و h ثابت اند و  فرمول استرلینگ

(که به غلط چنین نامگذاری شده است) و فرمول مشهور

که   ، همگی منسوب به اوست.

3.      مک لورن: دانشجویان رشته های علوم پایه و مهندسی با دو بسط معروف و بسیار مهم تیلور و مک لورن آشنایی دارند. بسط اول در ۱۷۱۵ و بسط دوم در ۱۷۴۲ معرفی شد. بسط مک لورن چیزی جز تعمیم بسط تیلور نیست و خود تیلور از بسط مک لورن خبر داشت و قبلا آنرا معرفی کرده بود. مک لورن از نوادر عالم ریاضیات بود. در ۱۱ سالگی وارد دانشگاه شد. در ۱۵ سالگی فوق لیسانس گرفت و در ۱۹ سالگی به استادی دانشگاه انتخاب شد. در ۲۱ سالگی کتاب مهم خود - هندسه ذاتی- را منتشر کرد و در ۲۷ سالگی استادیار دانشگاه بود. جالب است بدانیم که نیوتن برای اینکه مشکل پرداخت حقوق او حل شود و او در دانشگاه بماند، مخارج او را شخصا پرداخت می کرد تا دانشگاه از خدمات این نابغه قرن هجدهم بی بهره نماند. مک لورن بعدها جانشین نیوتن شد. 

4.      اویلر: لئونهارت اویلر پرتالیف ترین نویسنده در تاریخ ریاضیات است و نام وی در هر شاخه ای از این علم دیده می شود. او در طول عمرش۵۳۰ کتاب و مقاله منتشر کرد. حتی نابینایی کامل او که در ۱۷ سال آخر عمر، سراغش آمد، اثری در شدت کار او نگذاشت و به کمک حافظه شگفت انگیز و توانایی تمرکز حواس حتی با وجود سرو صدای زیاد، کار خود را با دیکته کردن به یک منشی و نوشتن فرمولها روی یک تخته بزرگ، ادامه می داد. او شاگرد یوهان برنولی بود و ۳۱ سال در آکادمی سن پترزبورگ و ۲۵ سال در آکادمی پروس به کارهای علمی اشتغال داشت. او خارج از ریاضیات، در فیزیک، نجوم، پزشکی، گیاهشناسی، شیمی، الاهیات و زبانهای شرقی استادی برجسته بود و از تاریخ مدنی و ادبی کلیه اعصار و بسیاری از ملل با اطلاع بود و جالب است بدانیم که با این همه کار و مشغله علمی، ۱۳ فرزند داشت!!  فیزیکدانی او را چنین معرفی می کند: اویلر را می توان بدون هیچ اغراقی، تجسم آنالیز دانست. او بی هیچ تلاشی، محاسبات خود را انجام می داد درست به گونه ای که انسان نفس می کشد و عقاب خود را در هوا نگاه می دارد. به خلاصه ای از کارهای اویلر می پردازیم:

- رسمیت یافتن نمادهای   برای نماد تابع، e برای پایه لگاریتم طبیعی، r و R به ترتیب برای شعاع دایره محاطی و محیطی مثلث،  برای علامت مجموعیابی و  i  برای واحد انگاری  را به او مدیونیم.

- فرمول بسیار مهم   نیز از کارهای اوست.

-  در هندسه به خط اویلر مثلث برمی خوریم، در نظریه معادلات دانشجو روش اویلر را برای حل معادلات درجه چهارم فرا می گیرد و در نظریه اعداد، تابع فی اویلر نقشی مهم دارد. تابع گاما و بتا نیز منسوب به اویلر هستند. در معادلات دیفرانسیل، معادله معروفی به نام معادله دیفرانسیل اویلر و نیز در معادلات دیفرانسیل جزئی، قضیه اویلر درباره توابع همگن وجود دارد.

- او از اولین کسانی است که کسرهای مسلسل را ایجاد کرد و به طور قابل توجهی نظریه اعداد را غنا بخشید.

- او مقالات زیادی پیرامون تفریحات ریاضی مانند «بازی شطرنج» و «مربعهای لاتین» دارد.

- او در ریاضیات کاربردی مانند نظریه حرکت ماه، کشتی سازی و نظریه موسیقی نیز کار کرده است.

- او کتابهای درسی نیز تالیف می کرد، آنهم با نهایت وضوح، به تفضیل و کامل. کتابهای امروزی دانشگاهی، تقلیدی از سبک نوشتاری اویلر هستند.

5.      کلرو: او از اعجوبه های ریاضی بود. در سن ۱۱ سالگی مقاله ای درباره منحنی های درجه سوم و بعد از آن مقاله دیگری درباره هندیه دیفرانسیل نوشت و در ۱۸ سالگی یکی از اعضای آکادمی علوم فرانسه شد. در ۲۳ سالگی به همراه هیأتی علمی مشغول اندازه گیری طول یک درجه از یک نصف النهار زمین شد. درباره نظریه شکل زمین، نظریه ماه و بازگشت ستاره دنباله دار هالی کارهای زیبایی انجام داد. در معادله دیفرانسیل،معادله ای به نام معادله کلرو وجود دارد. پدر و برادر او نیز ریاضیدان بودند.

6.      دالامبر: او یکی از پیشگامان حل معادلات دیفرانسیل با مشتقات جزئی است. او در ریاضیات کاربردی و مبانی آنالیز ریاضی کارهای ارزشمندی دارد. دالامبر اعتقاد داشت که برای قرار دادن آنالیز بر یک شالوده محکم، به نظریه معتبری از حد توابع نیاز است ولی معاصرین او اعتنایی به این مطلب نکردند. او برای اثبات قضیه اساسی جبر - که هر چند جمله ای با ضرایب مختلط حداقل یک ریشه مختلط دارد - تلاش بسیار کرد به گونه ای که هم اکنون این قضیه در فرانسه به قضیه دالامبر معروف است. مطالب جالبی از دالامبر درباره ریاضیات نقل شده است. یکی از گفته های او را نقل می کنیم بدون اینکه درباره آن اظهار نظر کنیم: «تردید ندارم که اگر انسانها جدا از هم زندگی می کردند و در وضعیتی بودند که به چیز دیگری جز حفظ بقای خود نمی پرداختند، مطالعه علوم دقیقه را بر پروردن هنرهای دلپذیر ترجیح می دادند، زیرا به خاطر دیگران است که انسان در هنر به کمال می رسد ولی انسان به خاطر خویشتن، خود را وقف علوم دقیقه می کند. بنابر این به نظر من، در جزیره ای متروک یک شاعر به ندرت می تواند خود را مفید بداند، در حالی که یک ریاضیدان می تواند هنوز هم از غرور اکتشاف سرشار باشد. » 

7.      لامبرت: یوهان هاینریش لامبرت، ریاضیدانی با کیفیت عالی بود و قوه تخیل بسیار قوی داشت. پسر خیاط فقیری بود و عمدتاً پیش خود درس خوانده بود. او اولین کسی بود که اصم بودن عدد پی را به طور دقیق ثابت کرد. او نشان داد که اگر x گویای ناصفر باشد آنگاه  tan x  اصم است. حال چون ، پس عدد پی اصم است. بسط منظم نظریه توابع هذلولوی و نمادهای امروزی این توابع را مدیون او هستیم. او در منطق ریاضی و نیز هندسه نااقلیدسی نیز کار کرده است.

8.      لاگرانژ: احتمالا می توان لاگرانژ را اولین آنالیزدان واقعی دانست. بعضی از ریاضیدانان، لاگرانژ را حتی از اویلر نیز بزرگتر می دانند. نوشته های لاگرانژ کوتاهتر اما بسیار دقیقتر از نوشته های اویلر است. ظاهراً شعور ریاضی او نیز از اویلر قویتر بود. برای مقایسه این دو بد نیست بدانیم که می توان ریاضیدانان بزرگ را به دو دسته عملگران رسمی خبره و نظریه پردازان خبره تقسیم کرد که عده کمی نیز در هر دو دسته قرار دارند. با این دسته بندی اویلر در دسته اول، لاگرانژ در دسته دوم و گاوس دانشمندی سر آمد در هر دو دسته بود. عبارت معروف و جالبی از لاگرانژ نقل شده است که به ذکر آن می پردازیم: «یک ریاضیدان به فهم کامل هر بخش از کار خود دست می یابد مادام که چنان وضوحی به آن بخشیده باشد که بتواند آن را به نحو قاطعی به اولین شخصی که در معبر به او برمی خورد، توضیح دهد.»  مطالب دیگر پیرامون اعتقادات لاگرانژ را در قسمت مربوط به لاپلاس خواهیم آورد. جالب است بدانید ناپلئون بناپارت درباره لاگرانژ چنین اظهار نظر کرده است: «لاگرانژ برج رفیع علوم ریاضی است.»  حال به کارهای مهم او در ریاضیات می پردازیم: 

- نمادهای  برای مشتق اول، دوم و ... تابع f، به لاگرانژ منسوب است.

- او بنیانگذار اولین نظریه توابع با یک متغیر حقیقی است.

- لاگرانژ کتابی دارد به نام «در حل معادلات عددی از کلیه درجات» که در آن روشی برای تقریب ریشه های حقیقی یک معادله به کمک کسرهای مسلسل ارائه می دهد.

- سهم او در پیشرفت معادلات دیفرانسیل با مشتقات جزئی بسیار قابل توجه است.

-  او میل وافری به نظریه اعداد داشت و رساله های مهمی در زمینه نگاشت. او این قضیه مهم را که به نام خود او ثبت شد، اثبات کرد: هر عدد صحیح مثبت را می توان به صورت مجموع حداکثر ۴ مربع نوشت.

- بعضی از کارهای او در نظریه معادلات بعدها رهنمون گالوا در نظریه گروهها شد و قضیه مهمی به نام  قضیه لاگرانژ در این نظریه وجود دارد. 

9.      لاپلاس: لاپلاس را نیوتن فرانسه می خواندند زیرا او کتابی پنج جلدی پیرامون مکانیک سماوی تالیف کرد که همه کشفیات قبلی در این زمینه، همراه با سهم خود او را در بر می گرفت و مولف را به عنوان استادی بی رقیب در این موضوع متشخص کرد. او در احتمالات، معادلات دیفرانسیل و ژئودزی نیز کارهای برجسته ای انجام داده است. هم عصر لاگرانژ بود اما از بسیاری لحاظ با او تفاوت داشت. به طور مثال تفاوت بارزی در سبک آنها وجود دارد. «کار لاگرانژ هم در صورت و هم در معنی کمال دارد و فهم استدلالهای او آسان است؛ اما لاپلاس هیچ چیز را توضیح نمی دهد، به سبک اعتنا نمی کند و اگر قانع شود که نتایجش درست هستند، برهانی برای آن ارائه نمی کند یا برهان غلطی ارائه می کند.» یکی از منجمین متذکر شده است که هرگز نشد به یکی از عبارات «بنابر این آشکار است » لاپلاس بربخورم بی آنکه مجبور باشم ساعتها برای پر کردن این شکاف کار کنم تا آن را بفهمم و نشان دهم که این مطلب چگونه به سادگی آشکار است!! در نظر لاپلاس ریاضیات کوله ای از ابزار است که برای توضیح طبیعت به کار می رود؛ اما در نظر لاگرانژ، ریاضیات هنری والاست و دلیل وجودی آن، خود آن است. البته لازم است بدانیم که لاپلاس برای مبتدیان در تحقیقات ریاضی بسیار سخی بود و در موارد متعددی از انتشار کشف خود، اجتناب می کرد تا به یک مبتدی اجازه دهد که زودتر از او فرصت انتشار آن را داشته باشد. لاپلاس دقیقاً صد سال بعد از درگذشت نیوتن از دنیا رفت و بنابر روایتی آخرین کلمات او چنین بود: آنچه می دانیم بسیار کم و آنچه نمی دانیم به غایت زیاد است.  

10.   لژاندر: کار عمده لژاندر حول نظریه اعداد، توابع بیضوی، روش کمترین مربعات و انتگرالها متمرکز بود. شهرت او عمدتاً به خطر کتاب «اصول هندسه» اوست که در آن قضایای هندسه اقلیدس مجدداً تنظیم و ساده شده است. بعدها این تالیف به صورت نمونه کتاب درسی در آمریکا درآمد و ترجمه انگلیسی آن ۳۳ مرتبه تجدید چاپ شد. نام لژاندر امروزه با یک معادله دیفرانسیل مرتبه دوم و جواب این معادله یعنی توابع لژاندر و چندجمله ایهای لژاندر و نیز در نظریه اعداد با نماد معروف لژاندر پیوند خورده است. او یک کتاب ۸۵۹ صفحه ای در دو جلد در نظریه اعداد دارد که اولین کتابی است که منحصراً به نظریه اعداد اختصاص دارد. او همچنین کتابی به نام «تمرینهای حساب انتگرال» نوشت که به علت جامعیت و قابل درک بودن با اثر مشابه اویلر برابری می کند. او به خاطر مثلث بندی کشور فرانسه به شهرت قابل توجهی دست یافت.

11.   مونژ: گاسپار مونژ در 16 سالگی معلم فیزیک مدرسه ای شد که خود در آن درس خوانده بود. او با ابداع هندسه ترسیمی - که نمایش اشیاء سه بعدی به کمک تصاویر دو بعدی است -  معروف شد. او در دانشگاه فیزیک نیز تدریس می کرد و معلمی با استعداد استثنایی بود. مونژ را پدر هندسه دیفرانسیل می دانند. اثر او تحت عنوان «کاربرد آنالیز در هندسه» پنج بار چاپ شد و یکی از مهمترین مباحث اولیه هندسه دیفرانسیل رویه ها بود. او در این اثر، مفهوم خطوط انحنای یک رویه در فضای سه بعدی را معرفی کرد. همچنین مطالبی که هم اکنون در هندسه تحلیلی فضایی مانند بررسی خطها و صفحات در فضا، فرمولهای انتقال و دوران محورها، فاصله یک نقطه از یک خط در فضا و کوتاهترین فاصله بین دو خط متنافر بررسی می شود از کارهای مونژ است. جالب است بدانید که او دوست نزدیک ناپلئون و به شدت و در همه حال به او وفادار بود چه زمانی که ناپلئون بناپارت سرجوخه ای آرمانگرا و انقلابی بود و چه زمانی که امپراطوری خود خواه و مستبدی شد. مونژ مدتی به عنوان وزیر نیروی دریایی وارد خدمت شد و به ساختن اسلحه و باروت برای ارتش پرداخت. او دو برادر داشت که آنها نیز استاد ریاضیات بودند.

12.   کارنو: او یکی از دانشجویان مونژ بود و او نیز شغل نظامی داشت. همانند استادش هندسه دان بود و برای اولین بار کمیتهای جهت دار را در هندسه ترکیبی به کار گرفت. یکی از کارهای کارنو پیدا کردن حجم یک چهار وجهی بر حسب شش یال آن بود. در ضمن فرمولی شامل ۱۳۰ جمله به دست آورد که هر یک از ۱۰ پاره خط واصل بین دو نقطه از ۵ نقطه تصادفی در فضا را بر حسب ۹ پاره خط دیگر بیان می کند. کارنو پسری داشت به نام «سعدی» که بعدها فیزیکدان برجسته ای شد. او به دلیل علاقه ای که به سعدی شیرازی داشت پسر خود را چنین نامگذاری کرد. نوه ای هم به نام سعدی داشت که رئیس جمهور فرانسه شد. کارنو بر خلاف مونژ بر علیه ناپلئون رای داد و راهی تبعیدگاه شد.

13.   سوفی ژرمن: این قرن شاهد ورود جدی زنان به پهنه های ریاضیات بود. سوفی ژرمن به علت زن بودن از ثبت نام در «اکول پلی تکنیک» - یکی از معروفترین دانشگاهای فرانسه- منع شد؛ اما یادداشتهای اساتید زیادی از آنجا را تهیه می کرد و حتی با اسمی مستعار مقالاتی نوشت که تحسین لاگرانژ را برانگیخت. او حتی بعدها مورد تعریف و تمجید گاوس نیز قرار گرفت. در سال ۱۸۱۶ آکادمی فرانسه به خاطر مقاله ای در نظریه ریاضی کشسانی، جایزه ای به وی اعطا کرد. او مفهوم انحنای میانگین را به هندسه دیفرانسیل رویه ها معرفی کرد.

 

خلاصه ای از تاریخچه ریاضی و ریاضیدانان(ریاضیات در قرن ۱۷ میلادی)

۷. ریاضیات در قرن ۱۷ میلادی

---

این قرن یکی از مهمترین قرنها در تاریخ ریاضیات است زیرا اساساْ دامنه تحقیقات گسترده در ریاضی، در همین قرن بر بشر گشوده شد، شاید به دلیل آزادیهای فکری بیشتر، پیشرفتهای سیاسی، اقتصادی و اجتماعی و در نتیجه رفاه بیشتر زندگی-به ویژه در مقابل سرما و تاریکی شمال اروپا.
پیشرفت علم ریاضی در این قرن آنقدر وسیع و گوناگون است که حتی نوشتن خلاصه ای از آن نیز مثنوی هفتاد من کاغذ خواهد شد. به ناچار باید به گزینش بعضی از کارهای اصیلتر و مهم تر در تاریخ ریاضی این قرن تن داد. از مهمترین اکتشافات - و شاید هم اختراعات - ریاضی در این قرن می توان به مطالب زیر اشاره کرد:

الف) کشف لگاریتم

ب) تدوین علامات و نمادگذاریهای کنونی جبری

ج) گشوده شدن پهنه جدیدی در هندسه محض به ویژه هندسه تصویری

د) آغاز اتصال جبر و هندسه با کشف هندسه تحلیلی

ه) پیشرفتی شگرف در نظریه اعداد و نیز تولد نظریه احتمال

و) کشف یکی از بزرگترین دستاوردهای بشر یعنی حساب دیفرانسیل و انتگرال

شاید بهترین راه برای بررسی تاریخ ریاضی این قرن، شرح مختصری از زندگانی ریاضیدانان برجسته قرن هفدهم باشد.

ریاضیدانان برجسته قرن هفدهم:

1.      نپر: چهار اختراع، بشر را در فن محاسبه چیره دست کرد: نماد گذاری هندی-عربی، چگونگی محاسبه مربوط به کسرها، لگاریتم و رایانه ها. «جان نپر» سومین اختراع را به نام خود ثبت کرد. او به طرز عجیبی، هم سیاسی و هم مذهبی بود و نبوغ او در پیشگویی وسایل جنگی چهار قرن بعد از خود اعجاب آور است. تعریف لگاریتم به وسیله نپر، بیشتر فیزیکی است تا ریاضی. بد نیست بدانیم که پایه لگاریتم نپر بر خلاف تصور عموم، عدد e نیست بلکه معکوس e است که البته خود او چیزی در این زمینه نمی دانست. تذکر این نکته لازم است که در تکمیل مفهوم لگاریتم و جداول مربوط به آن، «هنری بریگز» که یکی از دوستان نپر بود، سهم بسزایی دارد و لگاریتم معمولی در پایه ۱۰ را معمولاْ «لگاریتم بریگزی» می نامند. لگاریتم به معنای «عدد نسبت» است که البته این مفهوم، همان طور که ذکر شد بر اساس تابع توانی -که هم اکنون تدریس می شود- به وجود نیامد و یکی از امور خلاف قاعده در تاریخ ریاضیات، کشف لگاریتم، پیش از به کار بردن نماهاست. البته سه اختراع مهم دیگر نیز در تاریخ ریاضی، به نام جان نپر به ثبت رسیده است. (مراجعه کنید به صفحه ۴ جلد دوم کتاب تاریخ ریاضیات هاوارد د. ایوز.)
 

2.      پاسکال: این نابغه فرانسوی، یکی از بنیانگذاران هندسه محض و پیشرفته و نیز نظریه احتمال است. خواص اصلی اشکال معروف هندسی را در کودکی، بدون معلم و فقط با تلاشهای خودش به دست آورد. در شانزده سالگی مقاله ای درباره مقاطع مخروطی نوشت و در هجده یا نوزده سالگی، اولین ماشین حساب مکانیکی را اختراع کرد. اما متاسفانه در طول ۳۹ سال زندگی، به دلیل افراط و تفریطهای مذهبی، جسم ضعیف خود را بارها و بارها آزرد و چندین بار از ریاضیات دست کشید و دوباره به آن بازگشت. پاسکال را به عنوان یکی از بزرگترین «چه ها که می شد!!» در تاریخ ریاضیات شمرده اند. بعضی از کارهای او عبارتند از:

- تالیف مقاله مهمی درباره خواص اصلی مثلث خیام-پاسکال که در آن به طور جالبی از قدیمی
  ترین احکام قابل قبول استقرای ریاضی استفاده شده است.

- کشف و اثبات قضیه مشهور «هگزاگرام رمزی» که درباره یک ۶ ضلعی محاط در یک مقطع
  مخروطی است.

- پی ریزی علم احتمال به همراه «فرما» (ریاضیدان بزرگ فرانسوی). این علم به وسیله مکاتباتی
  بین پاسکال و فرما در تلاش برای حل «مساله امتیازها» در یک بازی شانسی به وجود آمد.

- اثری درباره منحنی سیکلوئید. این منحنی توسط نقطه ای واقع بر محیط یک دایره، هنگامی که
  دایره در امتداد خط مستقیمی بدون اصطکاک می غلطد، رسم می شود. این منحنی دهها
  خواص جالب و بسیار زیبا دارد و اختلافات بسیاری بین ریاضیدانان ایجاد کرد به طوری که به آن
  «سیب نفاق» گفتند (این نام بر اساس یک افسانه یونانی انتخاب شده است، برای مطالعه آن
  به پاورقی صفحه ۲۷ جلد دوم کتاب تاریخ ریاضیات هاوارد د. ایوز مراجعه فرمایید).  جالب است
  که از دوران این منحنی حول محور طولها، چیزی شبیه به سیب ایجاد می شود. 

3.      دکارت: دکارت را معمولاْ مبدع هندسه تحلیلی می دانند که از روشهای جبری برای حل مسائل هندسی استفاده می کرد. این کار کمک بسیاری در ساده سازی مفاهیم هندسی و حل مطالب غامض و پیچیده آن کرد. او همچنین به حل معادلات با درجات بالاتر از ۲ پرداخت و قاعده زیبایی را به نام «قاعده علامات دکارت» برای تعیین تعداد ریشه های مثبت و منفی یک چند جمله ای به دست آورد(مراجعه کنید به صفحه ۷۰ جلد دوم کتاب تاریخ ریاضیات هاوارد د. ایوز). او برای اولین بار از روش ضرایب نامعین استفاده کرد که همان متحد قرار دادن دو چند جمله ای هم درجه برای به دست آوردن ضرایب نامعین است. البته دکارت در جهان بیرون از ریاضیات، فیلسوف بسیار مشهوری است و مطالب بسیاری را به جهان فلسفه تقدیم کرده است که البته بعضی از آنها کاملاْ نادرست هستند. در ضمن داستانهای جالبی درباره چگونگی کشف هندسه تحلیلی به او نسبت می دهند که ارزش آموزشی زیادی دارد (مراجعه کنید به صفحه ۵۰ جلد دوم کتاب تاریخ ریاضیات هاوارد د. ایوز).
 

4.      فرما: معمولاْ فرما را بزرگترین ریاضیدان قرن هفدهم فرانسه می دانند. او حقوقدان بود و شغل رسمیش وکالت بود، اما قسمت مهمی از ساعات فراغت خود را وقف ریاضیات می کرد. او در بسیاری از شاخه های ریاضیات کارهای مهم و اساسی انجام داده است که مهمترین این کارها عبارتند از:

- تحقیقات اساسی پیرامون هندسه تحلیلی. فرما را باید در کنار دکارت یکی از موسسان
  هندسه تحلیلی نامید. معمولاْ گفته می شود که کارهای فرما عکس کارهای دکارت بوده است.
  دکارت از مکان هندسی شروع می کرد و به معادله آن می رسید، اما فرما از معادله شروع و
  سپس مکان هندسی آن را مطالعه می کرده است.

- تاسیس نظریه نوین اعداد. فرما شهود و توانایی خارق العاده ای در نظریه اعداد داشت. قضایای
  بسیاری را در این زمینه با اثبات یا بدون اثبات بیان کرد که بعدها درست بودن اغلب قضایای ثابت
  نشده او به ثبوت رسید(مراجعه کنید به صفحه ۵۲ و ۵۳ جلد دوم کتاب تاریخ ریاضیات هاوارد د.
  ایوز). حدس مشهور او به نام «حدس آخر فرما» در آخرین دهه قرن بیستم به اثبات رسید!  

- فرما به همراه پاسکال اساس علم احتمال را پی ریزی کرد.

- فرما در حساب دیفرانسیل نیز کارهای اساسی کرد. او ظاهراْ اولین کسی بود که از طریق
  معادله f'(x)=0 نقاط ماکزیمم و می نیمم یک تابع را به دست آورد(مراجعه کنید به صفحه ۹۳
  جلد دوم کتاب تاریخ ریاضیات هاوارد د. ایوز). همچنین او یک روش کلی برای یافتن مماس بر
  نقطه ای از یک منحنی که مختصات دکارتی آن معلوم باشد، ابداع کرد(مراجعه کنید به صفحه ۹۳
  جلد دوم کتاب تاریخ ریاضیات هاوارد د. ایوز).

5.      ریاضیدانان معروف قرن ۱۷ که قبل و یا همزمان با نیوتن می زیستند و در شکل گیری و پیشرفت
حساب دیفرانسیل و انتگرال نقش بسزایی داشتند: (۱) سیمون استوین (۲) لوکا والریو (این دو همان روشی را به کار بردند که ما برای پیدا کردن حجم یک جسم در حساب انتگرال به کار می بریم.) (۳) کاوالیری (۴) فرما (۵) جان والیس (نماد معروف بی نهایت را نیز به او مدیونیم.) (۶) آیزاک برو (که احتمالاْ قضیه اساسی حسابان را اولین بار او ثابت کرد.)

6.      نیوتن: صحبت کردن پیرامون نیوتن و کارهای او ساده نیست. ریاضیدان و فیزیکدانی که به گفته لاگرانژ بزرگترین نابغه ای است که در جهان زیسته است. همچنین «لایبنیتز» رقیب سرسخت او در ستایشی بزرگ منشانه، نیمی از کارهای انجام شده ریاضی بشر تا عهد نیوتن را متعلق به نیوتن می داند. انسانی که در ۲۳ سالگی به درجه ای رسید که می توانست مماس و شعاع انحنا در یک نقطه از منحنی را پیدا کند. روشی که امروزه تحت عنوان حساب دیفرانسیل شناخته می شود. در ۲۷ سالگی به استادی دانشگاه برگزیده شد و حدود ۶۵ سال در ریاضیات و فیزیک کار کرد. پاپ دستاوردهای نیوتن را بدین صورت بیان کرده است: «طبیعت و قوانین طبیعت در ظلمت نهفته بودند، ذات باری فرمود نیوتن به وجود آید و همه چیز روشن شد.» البته نیوتن نیز خاضعانه در مقابل ستایشها می گفت که من همچون کودکی در حال بازی در کنار دریا هستم که گاهی صدفهای زیبایی توجهم را جلب می کند اما اقیانوسی از حقایق کشف ناشده در مقابلم قرار دارد. یکبار هم گفت که اگر افق دید او گسترده تر از دیگران است بدین علت است که بر دوش غولان ایستاده است و شاید منظور او از غولان، ارشمیدس و امثال او باشند. کارهای ریاضی او به طور خلاصه به شرح زیر است:

- تالیف کتاب« اصول ریاضی فلسفه طبیعی» که با اصرار «هالی» ستاره شناس معروف و با هزینه او در سال ۱۶۸۷ چاپ شد. این کتاب به مطالعه دستگاه دینامیکی پدیده های زمینی و سماوی می پردازد و یک صورت بندی ریاضی از این پدیده هاست. این کتاب پرنفوذ ترین اثر در تاریخ علم به حساب می آید و تاثیر بسیاری بر دنیای جدید داشت. تاریخ ریاضیات ابتدایی اساساْ با آن پایان می یابد.

- بسط روش بی نهایت کوچکها یا همان حساب دیفرانسیل و نیز روشهای مربوط به  سریهای نامتناهی

- بسط روشهای مربوط به ماکزیمم و می نیمم توابع، مماس بر منحنی ها، انحنای منحنی ها، نقاط عطف، تحدب و تقعر منحنی ها، محاسبه مساحتهای زیر منحنی ها و طول قوس آنها

- ارائه روشی برای تقریب زدن مقادیر ریشه های حقیقی یک معادله جبری یا غیر جبری و نیز روشهای زیبایی برای مطالعه منحنی های درجه سوم

7.      لایبنیتز: این نابغه جامع ریاضیات، فلسفه، الاهیات و حقوق، رقیب جدی نیوتن در ابداع حسابان بود. عقیده رایج امروز این است که نیوتن و لایبنیتز، حسابان را مستقل از یکدیگر کشف کردند، اما لایبنیتز نتایج را زودتر انتشار داد، هر چند که کشف نیوتن زودتر انجام شده است، اما متاسفانه مشاجره اسفباری بین این دو بر سر تقدم در کشف حسابان در گرفت و هر کدام خود را موسس حساب دیفرانسیل و انتگرال می دانست. هر دو نیز در این مناقشه زیان دیدند، به ویژه نیوتن و ریاضیدانان همعصر او در انگلستان. البته لازم است ذکر شود که لایبنیتز را بزرگترین نابغه جامع قرن هفدهم می نامند و ظاهراْ تنها شخص شناخته شده تاریخ ریاضیات است که هم در ریاضیات پیوسته و هم در ریاضیات گسسته دارای اندیشه ای عالی بوده است. بد نیست بدانیم که لایبنیتز در واقع یک سیاستمدار و یک دیپلمات بود که برای انجام کارهای سیاسی به کشورهای دیگر سفر می کرد. کارهای او در ریاضیات به طور خلاصه عبارتند از:

- ارائه قسمت مهمی از نمادهای کنونی ما در حساب دیفرانسیل و انتگرال از قبیل نماد dx و dy/dx و علامت انتگرال که از S کشیده Summa -یک کلمه لاتین به معنای مجموع- اقتباس شده است. هم اکنون از نمادهای نیوتن آنچنان استفاده نمی شود.

- استخراج بسیاری از قواعد مقدماتی مشتق گیری که معمولاْ در ابتدای درس مشتق در سطوح مختلف دبیرستانی و دانشگاهی آموزش داده میشود. قاعده یافتن مشتق n-ام حاصلضرب دو تابع را قاعده لایبنیتز می نامیم (مراجعه کنید به صفحه ۱۱۳ جلد دوم کتاب تاریخ ریاضیات هاوارد د. ایوز).

- تلاش برای پایه گذاری نظریه پوشها و تعریف دایره بوسان برای اولین بار

- ارائه اولین ایده ها در منطق ریاضی و نظریه مجموعه ها. او مجموعه تهی و احتوای مجموعه ها را نیز مطالعه کرده است و متوجه شباهتهای نظریه مجموعه ها و منطق ریاضی شده است (به طور مثال شباهت قوانین دمرگان در نظریه مجموعه ها و منطق).

- لایبنیتز احتمالا جزو اولین ریاضیدانانی است که نظریه قدرتمند دترمینانها را برای حل دستگاه معادلات خطی پدید آورده اند.

 

خلاصه ای از تاریخچه ریاضی و ریاضیدانان(ریاضیات اروپایی- قرون ششم تا آخر قرن شانزدهم)

۶. ریاضیات اروپایی- قرون ششم تا آخر قرن شانزدهم

---

(الف) قرن ششم تا قرن یازدهم:

در طول پانصد سال که به عصر تاریکی اروپا شهرت دارد و با سقوط امپراطوری رم در اواسط قرن پنجم شروع شد و تا قرن یازدهم ادامه یافت، تقریباْ کار خاصی در علم به طور عام و در ریاضیات به طور خاص انجام نشد. از ریاضیدانان این دوران، معمولاْ از چهار نفر نام می برند که عبارتند از: بوئتیوس، بید، آلکوین و پاپ سیلوستر دوم نام می برند. این چهار نفر با تالیف کتب ریاضی - که معمولاْ بسیار ضعیف بودند - و تدریس آنها، در تاریخ ریاضیات این دوران بسزایی ایفا کردند. جالب است بدانیم  که پاپ سیلوستر دوم در مدارس مسلمانان اسپانیا درس خوانده بود.

(ب) قرن دوازدهم:

 از اوایل قرن دوازدهم میلادی، آثار یونانی و اسلامی به اروپای غربی انتقال یافت و این قرن در تاریخ ریاضیات، به قرن مترجمین بدل شد. اصول اقلیدس، المجسطی بطلمیوس و جبر خوارزمی به لاتین ترجمه شدند و دستگاه شمار هندی-عربی در اروپای غربی رواج یافت.

(ج) قرن سیزدهم و چهاردهم:

معمولاْ از «لئوناردو فیبوناتچی» به عنوان با استعدادترین ریاضیدان اروپا در قرن سیزدهم یا حتی قرون وسطی نام می برند. او در ایتالیا به دنیا آمد و در الجزایر بزرگ شد. در سفرهایش به مصر، سیسیل، یونان و سوریه مطالب بسیاری آموخت و پس از مراجعت به وطنش ایتالیا، بزرگترین کتاب خود به نام «کتاب حساب» یا «لیبرآباکی» را منتشر کرد. این کتاب که تاثیر بسیاری بر ریاضیات اروپای غربی داشت، ظاهراْ براساس جبر خوارزمی و ابوکامل نوشته شده است، هر چند که تحقیق مستقلی در حساب و جبر مقدماتی است. دنباله معروف فیبوناتچی در همین کتاب معرفی شده است. او دو کتاب دیگر به نامهای «هندسه عملی» و «کتاب مجذورات» نوشت که این آثار فراتر از تواناییهای اغلب فضلای معاصر وی بودند. البته  گفته شده است که شهرت بسیار فیبوناتچی، به دلیل فقدان معاصرین همتا با وی در اروپا بوده است نه به دلیل ویژگیهای علمی بالای آثار او.
لازم است که بدانیم قرن سیزدهم، شاهد ظهور دانشگاههای پاریس، آکسفورد، کیمبریج، پادوآ و ناپل است که بعضی از آنها به تقلید از دانشگاههای اسلامی بنا شده است.
در قرن چهاردهم که به قرن «مرگ سیاه» معروف است، کار قابل ملاحظه ای در ریاضیات انجام نشد جز نشانه هایی از پیدایش هندسه مختصاتی نوین و نیز مفاهیم اساسی پیوستگی و گسستگی و نیز مفاهیم بی نهایت کوچک و بزرگ.

(د) قرن پانزدهم و شانزدهم:

تاریخ قرن پانزدهم با آغاز رنسانس اروپا، زوال امپراطوری بیزانس به دست مسلمین، انتشار آثار کلاسیک یونان به زبان اصلی، اختراع صنعت چاپ که نشر دانش را با سرعتی بی سابقه میسر کرد و کشف قاره آمریکا که کشتیرانی دور کره زمین و فعالیتهای تجاری را افزونتر کرد، عجین شده است. این وقایع خود به خود بر پیشرفت ریاضیات اثر بسیار نهادند. در این قرن کم کم شاهد ظهور علامات + و -- (جمع و تفریق) و نیز استفاده از علاماتی برای مختصر نویسی ریاضی هستیم. 

قرن شانزدهم شاهد یکی از کارهای مهم در تاریخ ریاضیات است. در این قرن نمادگرایی در جبر آغاز شد. نماد معروف تساوی در این قرن به کار گرفته شد که علامت یک جفت پاره خط موازی و مساوی است. به قول «رکورد» که اولین بار آنرا به کار برد، هیچ دو شیئ نمی توانند مساوی تر از این باشند. نماد رادیکال نیز در همین قرن ابداع شد. احتمالاْ این نماد به جهت شباهت آن به r و به نشانه radix (ریشه) به کار گرفته شده است. در قرن شانزدهم اعداد منفی نیز مورد توجه قرار گرفتند.
در این قرن، از ریاضیات برای مقاصد اعتقادی نیز استفاده می شد. به عنوان مثال، از ریاضی حتی برای تفسیر آیات انجیل و تورات استفاده کردند.

احتمالاْ جالبترین دستاورد ریاضی قرن شانزدهم، کشف راه حل جبری معادلات درجه ۳ و ۴  توسط چهار ریاضیدان ایتالیایی است که عبارتند از: «فرّو»،«تارتاگلیا»، «کاردانو» (یا کاردان) و «فراری». داستان این کشف و نیز زندگانی این ریاضیدانان، یکی از خواندنی ترین فرازهای تاریخ ریاضیات است که چون هدف ما بیان خلاصه ای از وقایع تاریخ ریاضی است، از شرح آن - البته با اکراه- می گذریم. برای مطالعه آن به صفحات ۲۶۶ تا ۲۷۱ جلد اول تاریخ ریاضیات هاوارد د. ایوز مراجعه فرمایید. 

بالاخره باید از بزرگترین ریاضیدان فرانسوی این قرن، «فرانسوا ویت» نام برد که سهم قابل ملاحظه ای در پیشرفت مثلثات دارد. او جبردان برجسته ای نیز بود و روشی برای تقریب ریشه یک معادله ارائه و معادله درجه ۳ را به روشی غیر از روش کاردان-تارتاگلیا حل کرد.نمادهای خاصی را نیز هنگام نوشتن به کار می برد. مثلاْ به جای a²  و  a³  می نوشت: aa و aaa.

البته لازم است بدانیم که در این قرن چند جدول عالی برای محاسبه نسبتهای ششگانه مثلثاتی تالیف شد که بعضی از آنها تا ۱۰ رقم اعشار دقت داشتند و محاسبه آنها ۱۲ سال طول کشید.

خلاصه ای از تاریخچه ریاضی و ریاضیدانان(ریاضیات دوره اسلامی)

۵. ریاضیات دوره اسلامی 

---

آغاز و انجام تمدن اسلامی یکی از عجیب ترین وقایع تاریخ بشر است. مردمی که قرنها در توحش می زیستند، سواد در میان آنها محلی از اِعراب نداشت، دختران خود را زنده به گور می کردند، بدترین غذاها را می خوردند و دائماْ در حال نزاع قبیله ای بودند، فقط در عرض حدود ۹۰ سال، تمدنی را بر پا کردند که از کرانه های سند در هندوستان تا شمال افریقا و اسپانیا امتداد داشت. تمدنی که فراگرفتن علم و دانش را جهاد راه خدا می دانست و در کتابخانه های آن هزاران جلد و در بعضی از آنها حدود چهار صد هزار جلد کتاب موجود بود- مانند کتابخانه سلطنتی امیر قرطبه. به قول جواهر لعل نهرو، در بعضی از مناطق این تمدن پهناور، تقریباْ همه سواد خواندن و نوشتن داشتند و بعضی از شهرهای آن بالغ بر یک میلیون نفر جمعیت داشت با تمام امکانات رفاهی لازم. مسلمانان علوم دقیقی همچون ریاضی، فیزیک، شیمی، مهندسی، پزشکی، نجوم و دریانوردی را با علوم معنوی همچون فلسفه، منطق، حکمت و عرفان پیوند داده بودند. چنین تمدنی- اما - به دلیل دور شدن مسلمین از احکام زیبای اسلام، کم کم رو به زوال نهاد و جای خود را به تمدن غرب داد.
تمدن غرب به گواهی صدها سند و مدرک، وجود خود را مدیون تمدن اسلامی است. اما ریاکارانه سعی در پنهان کردن این دین و کم اهمیت جلوه دادن تمدن بزرگ اسلامی داشته و دارد. غربیها - جز اندکی از دانشمندان منصف آن- سعی دارند که چنین جلوه دهند که تنها نقشی که تمدن هفتصد ساله اسلامی دارد، همانا محافظت از علوم یونانی و انتقال آنها به اروپاست که توهینی بس بزرگ به این تمدن شکوهمند و دروغی کاملا آشکار است.

با نگاهی به کتاب تاریخ ریاضیات هاوارد د. ایوز که در حال حاضر یکی از منابع مهم دانشگاهی کشور در درس تاریخ ریاضی است، می توان بارها و بارها این بی انصافی را مشاهده کرد. به طور مثال وقتی از تمدن اسلامی صحبت می کند با دهها دانشمند عالیمقام آن، تنها حدود ۱۵ صفحه را به آن اختصاص می دهد، اما برای تشریح تاریخ ریاضیات قرون وسطی - یا به قول خودشان قرون تاریکی - تا آخر قرن شانزدهم که مدت آن حدود ۱۰۰۰ سال و کارهای اصیل ریاضی در آن کم است، ۴۷ صفحه از کتاب را پر می کند و حتی گاهی به جزئیات کتابهای ریاضیدانان این عصر می پردازد. به طور مثال رجوع کنید به صفحات ۲۵۵ و ۲۵۶ (جلد اول، ویرایش دوم) که درباره «لیبرآباکی»، کتاب مشهور فیبوناتچی صحبت می کند( کتابی که اساساْ کپی هنرمندانه ای از آثار خوارزمی و ابوکامل به همراه تحقیقات اوست) یا اواخر صفحه ۲۵۹ و اول صفحه ۲۶۰ که درباره کتاب رگیومانتوس صحبت می کند و نیز شکل صفحه ۲۶۵. در اینباره حرف بسیار است و درد دل فراوان که انشاءالله در وقت و جای مناسب درباره آن مفصلاْ و به طور کاملاْ مستند صحبت خواهیم کرد. «قضاوت منصفانه را به خواننده واگذار می کنیم.» 

حال به خلاصه ای از مطالب کتاب هاورد ایوز درباره ریاضیات دوره اسلامی می پردازیم. البته همان طور که توضیح داده شد، این مطالب کاملاْ گزینشی و بسیار ناقص است که به در حد توان این نقایص را رفع خواهیم کرد. برتری تمدن اسلامی بر سایر تمدنها حدودا از سال ۷۰۰ میلادی آغاز گردید و حدودا تا سال ۱۵۰۰ میلادی که اسپانیا از تسلط مسلمین خارج شد، ادامه یافت. از همان ابتدا، خلفا به حامیان علم مبدل شدند و دیگران را تشویق کردند که آثار هندی و یونانی را در نجوم، طب و ریاضیات به زبان عربی برگردانند. در نتیجه بسیاری از علوم یونانی و هندی بدین طریق سالم ماند و در قرون وسطی از میان نرفت. به طور خلاصه به شرح بعضی از کارهای مسلمین در ریاضیات می پردازیم:

1.      ترجمه المجسطی (اثر بطلمیوس) و اصول قلیدس از یونانی به عربی

2.      تالیف کتاب الجبر و المقابله - که کلمه Algebra از همین کتاب اقتباس شده است- و کتابی درباره ارقام هندی - که بوسیله آن کلمه «آلگوریتم»، لاتینی شده کلمه «الخوارزمی»، به ریاضیات اضافه شد - توسط «محمد بن موسی خوارزمی». این دو کتاب تاثیر بسیار زیادی در پیشرفت ریاضیات اروپا داشتند.

3.      کارهای «ثابت بن قُره» در ترجمه بسیار خوب آثار یونانی و نیز کارهای او در جبر مقدماتی، مربعهای جادویی و یافتن اعداد متحابه که ظاهراْ از اولین کارهای اصیل ریاضیات توسط مسلمین است. او قضیه فیثاغورث را به روش زیبایی تعمیم داده است.(مراجعه کنید به صفحه ۲۴۳ جلد اول کتاب تاریخ ریاضیات هاوارد د. ایوز) 

4.      معرفی تابع تانژانت به وسیله «ابوالوفای بوزجانی». او جدول بزرگی از سینوس و تانژانت زوایا را برای محاسبات مثلثاتی به دست آورد.

5.      تالیف کتابی به نام «فخری» از «کرخی» یا «کرجی» که یکی از فاضلانه ترین کارهای مسلمین در جبر است. همچنین کرخی قضایایی ارائه کرد که مجموع مربعات و مکعبات اولین n عدد طبیعی را محاسبه می کرد.

6.      حل هندسی معادله درجه سوم توسط «عمر خیام» که یکی از عمیقترین و بدیعترین آثار جبری مسلمین است.

7.      تولد هندسه نا اقلیدسی با کارهای «خواجه نصیرالدین طوسی». مباحث او در این زمینه، حدوداْ ۴۵۰ سال بعد در قرن هفدهم میلادی در دانشگاه آکسفورد برای تدریس هندسه مورد استفاده قرار گرفت. برهان اصیلی نیز برای قضیه فیثاغورث به خواجه نصیر منسوب است.(مراجعه کنید به صفحه ۲۳۲ جلد اول کتاب تاریخ ریاضیات هاوارد د. ایوز)

8.      تقریب عدد پی تا ۱۶ رقم توسط «غیاث الدین جمشید کاشانی» که تا ۲۰۰ سال بعد از او کسی به دقت او در محاسبه عدد پی به روش کلاسیک نرسید. همچنین او کارهای جالبی درباره ارتباط بین قضیه دو جمله ای نیوتن و مثلث خیام-پاسکال انجام داده است.

9.      مسلمین کارهای زیادی برای حل معادلات سیاله انجام دادند. به عنوان مثال برهانی بر این قضیه ارائه کردند که مجموع مکعبات دو عدد طبیعی برابر مکعب هیچ عدد طبیعی نمی شود. این قضیه حالت خاصی از «آخرین قضیه فرما» است.

10.   بسیاری از نامها و واژه های کنونی را می توان در دوره مسلمین یافت. به طور مثال بد نیست بدانید که کلمه «سینوس» ترجمه لاتینی کلمه عربی «جَیب»، به معنای خلیج کوچک است.

خلاصه ای از تاریخچه ریاضی و ریاضیدانان(ریاضیات چین و هند)

۴. ریاضیات چین و هند

---

مختصری از تاریخ ریاضیات چین از حدود ۱۰۰۰ قبل از میلاد تا قرن ۱۴ بعد از میلاد:

-  چینیان باستان با حساب دهدهی آشنایی داشتند و از آن در محاسبات علمی و روزمره استفاده می
   کردند.

- ابداع مربعهای جادویی

- آنها با قضیه فیثاغورث -بدون برهان - آشنایی کامل داشتند.

- آنها «قضیه چینی» که قضیه مشهوری در جبر و درباره حل معادلات همنهشتی خطی است، به جهان
  ریاضیات تقدیم کردند.

- در بعضی از آثار آنها، محاسبه درست «عدد پی» تا ۶ رقم اعشار دیده می شود.

- احتمالاْ مثلث حسابی معروف «خیام-پاسکال»، اولین بار به وسیله چینیان ارائه شده است.


مختصری از تاریخ ریاضیات هندی از حدود ۴۵۰ میلادی تا قرن ۱۴ بعد از میلاد:
 
- معرفی عمل ضرب به شیوه کنونی

- به دست آوردن مجموع تصاعد های حسابی و هندسی

- آشنایی با اعداد منفی و گنگ

- حل کامل معادلات درجه ۲

- یافتن همه جوابهای بعضی از معادلات سیاله

- به دست آوردن فرمول هرون برای محاسبه مساحت مثلث و تعمیم آن به یک چهار ضلعی محاطی- 
  رجوع شود به صفحه ۲۲۵ جلد اول کتاب تاریخ ریاضیات هاوارد د. ایوز. 

- ساختن جداولی برای سینوسها

- سه ریاضیدان معروف قدیم هند «برهمگوپته»، «مهاویره» و «بهاسکره» هستند که به ترتیب در قرون
  هفتم، نهم و دوازدهم میلادی می زیستند. ریاضیدان معروف قرون جدید هند، نابغه هندی
  «رامانوجان» است که در نظریه اعداد کارهای بزرگی انجام داد و حدوداْ ۳۳ سال بیشتر عمر نکرد.

- سخن ابوریحان بیرونی :«ریاضیات هندی مخلوطی از صدف و خزف یا ممزوجی از درّ پر بها و
  سنگریزه بی بها است» (این جمله به خوبی نشان دهنده تسلط ریاضیدانان مسلمان است بر ریاضیات
  زمان خود که می توانستند ریاضیات عالی را از مقدماتی تمییز و درباره آن اظهار نظر کنند.)

 

خلاصه ای از تاریخچه ریاضی و ریاضیدانان(ریاضیات یونان باستان)

۳. ریاضیات یونان باستان

---

با شروع هزاره اول میلادی و با افول تمدن بزرگ مصر و بابل، کم کم تمدنهای جدیدی مانند تمدن یونانی، فنیقی و آسوری پا به عرصه وجود گذاشتند. با تکامل ذهنی بشر، انسان با کلمه «چرا» مانوس تر شد.

 - چرا زوایای متقابل به راس با هم برابرند؟
 - چرا در مثلث متساوی الساقین دو زاویه روبه رو به دو ساق برابرند؟
 - ...؟

به این ترتیب، ریاضیات برهانی متولد شد و یونانیان در این امر پیشتاز بوده اند. در این قسمت به طور بسیار خلاصه، به نام و کارهای ریاضیدانان یونانی به ترتیب زمانی خواهیم پرداخت.

1.      تالس یکی ریاضیدانانی است که برای اولین بار به وسیله استدلال منطقی و بدون  استفاده از شهود، چند قضیه مهم هندسه را ثابت کرد. (مراجعه کنید به صفحه ۶۵ جلد اول کتاب تاریخ ریاضیات هاوارد د. ایوز)

2.      فیثاغورس (یا به عبارت درست تر فیثاغورسیان که پیروان و شاگردان او بودند) نیز سهم بسزایی در تکامل ریاضیات برهانی داشت. خلاصه ای از کارهای فیثاغورسیان را مرور می کنیم:

(الف) این گروه اولین قدمها را در رشد نظریه اعداد برداشتند، مانند معرفی اعداد متحابه، تام، ناقص و زاید (مراجعه کنید به صفحه ۷۰ و ۷۱  جلد اول کتاب تاریخ ریاضیات هاوارد د. ایوز ) و نیز معرفی اعداد مصور مثلثی، مربعی، مخمسی (مراجعه کنید به صفحه ۷۲ تا ۷۴ جلد اول کتاب تاریخ ریاضیات هاوارد د. ایوز).

(ب) اولین برهان منطقی و درست از قضیه فیثاغورس که بابلیان قدیم بدون برهان از آن استفاده می کردند.

(ج) کشف عدد گنگ که یکی از حوادث مهم تاریخ ریاضیات است.

(د) ابداع جبر هندسی برای بیان اتحادهای جبری در قالب اصطلاحات هندسی. برای توضیح بیشتر، اتحاد 

 

 را به این وسیله با شکل زیر «ثابت» می کنیم:

(ه) حل هندسی معادلات درجه دوم. برای مثال با فرض اینکه a و b دو عدد مثبت باشند، طول x را چنان به دست می آوریم که x جواب معادله   باشد. این کار را در شکل زیر انجام داده ایم. (با این کار می توان برای هر عدد طبیعی n، را رسم کرد. کافیست دایره ای به قطر n+1 رسم کنیم.) 

 

(و) معرفی بعضی از اجسام پنجگانه افلاطونی یا اجسام منتظم پنجگانه (یک چند وجهی را منتظم گوییم اگر وجوه آن چند ضلعی های منتظم مساوی باشند و کنجهای آن نیز همگی برابر. )

(ز) بسط روش اصل موضوعی که اثبات یک ادعاست به وسیله سلسله استنتاجهای دقیق از چند فرض آغازین که کاملاْ مشخص هستند.

3.      افلاطون و شاگردان او: تقریباْ تمام کارهای مهم ریاضی قرن چهارم قبل از میلاد به وسیله شاگردان افلاطون انجام شده است و آنها حلقه ارتباط بین فیثاغورسیان و ریاضیدانان مکتب اسکندریه بودند. نظر افلاطون درباره ریاضییات این بود که این علم عالیترین زمینه را برای تعلیم ذهن فراهم می سازد و اداره کنندگان جامعه باید ریاضی بدانند. معروف است که افلاطون بر سر در آکادمی خود نوشته بود: «هر کس هندسه نمی داند وارد نشود.»

کارهایی که معاصران افلاطون انجام دادند:

(الف) کشف مقاطع مخروطی (مقاطع مخروطی معمولا شامل دایره، سهمی، هذلولوی و بیضی میشود.)

(ب) تضعیف مکعب (چگونگی ترسیم ضلعی از یک مکعب -فقط با خط کش و پرگار- که حجم آن مکعب دو برابر حجم مکعبی مفروض است.)

(ج) تثلیث زاویه (چگونگی تقسیم یک زاویه دلخواه به سه قسمت مساوی-فقط با خط کش و پرگار)

(د) تربیع دایره (چگونگی ساختن مربعی که دارای مساحتی برابر با مساحت دایره مفروضی باشد -فقط با خط کش و پرگار)

توضیح: توجه کنید که می توان ثابت کرد هیچکدام از کارهای بالا -یعنی تضعیف مکعب، تثلیث زاویه و تربیع دایره را نمی توان فقط به وسیله خط کش و پرگار انجام داد که داستان مفصل و جالبی برای خود دارد. همچنین توجه کنید که تربیع دایره پیوند نزدیکی با محاسبه عدد پی دارد (در صفحه  ۱۱۶ جلد اول کتاب تاریخ ریاضیات هاوارد د. ایوز،می توانید تاریخچه زیبایی از عدد پی را مشاهده فرمایید که شامل ۳۸ مدخل است از کارهای یونانیان، مسلمین، اروپائیان و ریاضیدانان عصر جدید درباره این عدد.)

4.      اقلیدس: او استاد ریاضییات دانشگاه اسکندریه بود و احتمالاْ در آتن یونان درس خوانده است. اقلیدس در دوران خود، به فروتنی و توجهش به دیگران معروف بود. بد نیست بدانیم که اسکندریه در آن زمان در حدود پانصد هزار نفر جمعیت داشت و دانشگاه آن بسیار بزرگ و مجهز به سالنهای سخنرانی، آزمایشگاه، خوابگاه و کتابخانه بود و در این کتابخانه حدوداْ ششصد هزار طومار پاپیروس وجود داشت و حدود هزار سال پابرجا ماند.

- اقلیدس حدود ۱۰ کتاب تالیف کرده است که مهمترین اثر او کتاب اصول اوست که شاید یکی از
  مهمترین کتابهای تمام تاریخ بشر باشد. لازم است بدانیم که این اثر به وسیله مسلمین به
  دست اروپائیان رسید و اروپائیان اصول اقلیدس را از عربی به لاتین ترجمه کردند.
  این کتاب شامل ۱۳ مقاله و حاوی ۴۶۵ قضیه درباره هندسه مسطحه، هندسه فضایی، نظریه
  اعداد و جبر مقدماتی هندسی است.
- قضایای معروف این کتاب: آلگوریتم اقلیدسی (برای تشخیص متباین بودن دو عدد)، قضیه اصلی
  حساب و اثبات این که تعداد اعداد اول بی نهایت است.
- احتمالاْ این کتاب تدوینی منظم و زیبا از آثار ریاضیدانان قبل از اقلیدس به همراه کارهای خود
  اقلیدس است و شاید قصد او از تالیف این کتاب این بوده است که یک کتاب درسی مقدماتی
  در ریاضی عمومی بنویسد. البته اقلیدس در ریاضیات عالی نیز کتابهای درسی تالیف کرده
  است.
- به نظر می رسد که مهمترین کار او در این کتاب آن باشد که سعی کرده است تمام ۴۶۵ قضیه را
  فقط بر اساس ۱۰ اصل موضوع اثبات کند.(مراجعه کنید به صفحه ۱۵۰ جلد اول کتاب تاریخ
  ریاضیات هاوارد د. ایوز) 
 

5.      ارشمیدس: اروپائیان معمولاْ «ارشمیدس»، «نیوتن» و «گاوس»  را بزرگترین ریاضیدانان همه اعصار می دانند. اگر این مطلب درست هم نباشد، ظاهراْ می توان گفت ارشمیدس بزرگترین ریاضیدان عهد باستان بود.

- حدوداْ در سال ۲۸۷ قبل از میلاد متولد شد و به احتمال قوی مقداری از عمر خود را در دانشگاه
  اسکندریه گذراند.

- درباره زندگانی ارشمیدس مطالب جالبی نقل شده است: دفاع از سیراکوز (شهر ارشمیدس)
  در مقابل سپاه روم و شکست رومیان فقط به وسیله اهرمها و جرثقیلها و نیز تمرکز ذهنی بسیار
  قوی بطوریکه هنگام حل مساله از اطراف خود کاملا بی خبر می شد- و همین بی خبری بالاخره
  باعث مرگ او شد.

- ارشمیدس سه کتاب درباره هندسه مسطحه، دو کتاب درباره هندسه سه بعدی، دو مقاله
  درباره نظریه اعداد، دو رساله (نامه)  درباره ریاضیات کاربردی (در واقع فیزیک ریاضی) و یک
  رساله (نامه) تحت عنوان «روش» دارد که روش او را در کشف بسیاری از قضایا شرح می دهد.
  این رساله در سال ۱۹۰۶ میلادی کشف شد.

- مقاله های ارشمیدس شاهکارهایی از بیان ریاضی هستند و تا حد قابل توجهی به مقاله های
  امروزی شباهت دارند.

- او در بسط اولیه مفاهیم انتگرال برای محاسبه مساحتها و حجمها نقش اساسی دارد.
  او روش کلاسیک برای محاسبه «عدد پی» را کشف کرد. در این روش با ترسیم چند ضلعیهای
  محاطی و محیطی برای دایره واحد، به تقریب جالبی برای «عدد پی» می رسیم.

- ارشمیدس - به ادعای ابوریحان بیرونی - کاشف فرمول مشهور «هرون» برای مساحت مثلث
  برحسب سه ضلع آن است.

- او در رساله ای درباره مقدار تقریبی دانه های شنی که کره ای به مرکز زمین و به شعاع زمین تا
  خورشید را پر نماید، صحبت کرده است.

- در رساله دیگری سعی می کند که یک معادله هشت مجهولی با مقادیر صحیح را که به وسیله
  هفت معادله خطی به هم مربوط شده اند، حل کند و یکی از جوابهای این معادله عددی است با
  بیش از «۲۰۶۵۰۰» رقم!!

6.      آپولونیوس: هندسه دان کبیر باستان و واضع رسمی مقاطع مخروطی که نامهای یونانی بیضی، سهمی و هذلولوی به وسیله او به این شکلهای هندسی داده شده است.

7.      دیوفانتوس: این ریاضیدان، دارای نبوغ عجیبی در نظریه جبری اعداد بود و مسائل ارائه شده توسط او در بسط جبر و نظریه اعداد اهمیت بسیاری دارند.
 

8.      پاپوس: شارح بزرگ آثار هندسه دانان یونانی که ما قسمت عمده دانش خود را از هندسه یونان باستان، به رساله بزرگ او مدیونیم.

 

خلاصه ای از تاریخچه ریاضی و ریاضیدانان(ریاضیات بابلی و مصری)

 

. ریاضیات بابلی و مصری

---

با پیشرفته تر شدن جامعه بشری، انسان به ریاضیات عملی برای کارهای کشاورزی، مهندسی، علوم مالی و بازرگانی، محاسبات مربوط به زمان و تقویم، سنجش اوزان و مقادیر و ... نیازمند شد. کم کم با تقویت ذهن بشر، انسان به تجرید گرایش پیدا کرد و ریاضیات را برای ریاضیات مورد مطالعه قرار داد و در نتیجه، تمدنهایی همچون بابل، مصر، چین و هند ایجاد شد. حال به بررسی مختصر تاریخ ریاضی بابل و مصر باستان می پردازیم به دودلیل: یکی اینکه این دو از پیشرفته ترین تمدنهای باستانی هستند و دیگر اینکه سندهای معتبری از ریاضیات تمدنهای مهم دیگر مانند چین و هند باستان در دست نیست. (البته در قسمتهای بعدی، مختصرا به  این دو تمدن نیز خواهیم پرداخت. ) 

ریاضیات بابلی:

·        بررسی لوحهای پخته، نشان از مهارت بسیار بابلیها در محاسبه دارد.  بسیاری از محاسبات عددی که برای انواع و اقسام قراردادهای رسمی و غیر رسمی مانند صورت حساب، رهن، قباله و ضمانت لازم بود، به کمک جداول انجام می شد، مانند جداول ضرب ، جداول معکوس اعداد،
جداول مربعات و مکعبات و جداول توانها. این محاسبات بر حسب دستگاه موضعی شصتگانی بوده اند. 

·        احتمالاْ بابلیها با با قواعد کلی محاسبه مساحتهای اشکال دو بعدی - مانند مستطیل، مثلث و ذوزنقه- و سه بعدی - مانند مکعب مستطیل- و حتی محاسبه مساحت دایره آشنا بوده اند و عدد پی را سه یا سه و یک هشتم در نظر می گرفته اند.

·        تقسیم محیط دایره به ۳۶۰ قسمت را مدیون بابلیها هستیم.

·        آنها احتمالا با قضیه فیثاغورس نیز آشنا بوده اند. در تجزیه و تحلیل لوح معروفی به نام پلیمپتن (Polimpton) مشخص شده است که آنها با سه تاییهای فیثاغورسی و جداول مثلثاتی به طور حیرت آوری آشنا بوده اند.

·        ظاهرا روش حل بعضی از معادلات درجه ۲، ۳ و حتی درجه ۴ را نیز می دانسته اند.

·        توجه کنید که ریاضیات ایران باستان را نیز می توان جزئی از ریاضیات بابلی دانست.

 ریاضیات مصر باستان:

·         آنگونه که از بررسی پاپیروسهای به جا مانده از مصریان قدیم می توان گفت این است که سطح ریاضی مصریان قدیم، هرگز به ریاضیات بابلی نرسید. بیشتر مسائل ریاضی باقیمانده از مصریان باستان، عددی و بسیار ساده هستند. اما از بعضی لحاظ، ریاضیات مصری را نمی توان نادیده گرفت. به طور مثال، مصریان از اعداد بزرگ مانند صدهزار و یک میلیون استفاده می کرده اند و دقت محاسبه ای که در ساختن اهرام مصر به کار رفته، واقعاْ حیرت آور است.

·        مصریان، ضرب و تقسیم اعداد را به گونه ای جالب انجام می دادند به طویکه نیازی به حفظ کردن جدول ضرب نبود.

·        مصریان سعی می کردند کسرها را به صورت مجموعی از کسرها با صورت یک بنویسند و به این وسیله مجموع کسرها را راحت تر به دست می آوردند.

·        احتمالاْ از تصاعدهای حسابی و هندسی نیز استفاده می کرده اند.

·        در جبر مصری تا حدی نماد گرایی نیز وجود داشت و نمادهایی برای جمع و تفاضل داشتند.

·        ظاهراْ قاعده محاسبه مساحت مثلث را می دانستند و با بعضی از نسبتهای مثلثاتی(مانند کتانژانت) آشنا بوده اند.

·        عدد پی را حدوداْ  ۳/۱۶ حساب می کردند.

·        ظاهراْ از قضیه فیثاغورس هیچ اطلاعی نداشتند، اما زاویه قائمه را با ساختن مثلثی به اضلاع ۳، ۴ و ۵ می ساختند.

بعضی از مسائل (همچون محاسبه درست هرم ناقص مربع القاعده) در پاپیروسهای مصری موجود است که نظیر آن در هیچ جای دیگری از شرق باستان، یافت نشده است

 

 

افلاطون

افلاطون که یکی از بزرگترین فلاسفه جهان به شمار می رود، در آتن در سال 428 ق. م، در یک خانواده متشخص آتنی متولد شد. نام اصلی او« آریستو کلس» بود و نام افلاطون، بعد ها به مناسبت پیکر تنومندش به او داده شد.

او در یک خانواده اشرافی بزرگ شد. دوره جوانی او همراه بود با دوره درخشندگی فرهنگ آتنی و در همان دوران، در سن بیست سالگی با سقراط ملاقات کرد و شاگرد او شد. بستگانش اصرار داشتند که او به حرفه خانوادگی خود یعنی سیاست بپردازد، اما وقتی محاکمه و مرگ استادش را به دست سیاستمداران مشاهده کرد، سیاست را رها کرد.

او در محاکمه سقراط حاضر بود و اتفاقات آن را در آثار خود ثبت کرده است.پس از مرگ استاد، افلاطون آتن را ترک و به مناطق مختلفی نظیر مگارا و سیسیل سفر کرد که خطرات بزرگی هم برایش در بر داشت؛ تا جایی که اسیر شد و حتی در معرض مرگ قرار گرفت؛ اما سرانجام آزاد شد و به آتن باز گشت.

وی در بازگشت به آتن در سال 388 ق.م، « آکادمی» خود را با هدف ترویج و تشویق بی طرفانه علم، در این شهر بنا کرد. آکادمی افلاطون را به حق می توان نخستین دانشگاه اروپایی نامید، زیرا در آنجا مطالعات و تحقیقات محدود به فلسفه محض نبود، بلکه رشته های وسیعی از علوم دیگر مانند ریاضیات، نجوم و علوم طبیعی را نیز در بر می گرفت. جوانان از شهر های دور و نزدیک به آن جا می آمدند و علوم مختلف را فرا می گرفتند. یکی از همین جوانان، ارسطو بود که بعدها در زمره بزرگ ترین فلاسفه جهان قرار گرفت.

افلاطون علاوه بر سرپرستی آکادمی و رهبری مطالعات، خود به تدریس نیز می پرداخت و شاگردانش از درس های او یادداشت بر می داشتند. بسیاری از آثاری که از او باقی مانده، حاصل این درسهاست.

شهرت و اعتبار افلاطون به عنوان یک فیلسوف بزرگ و آگاه، سبب شد تا حاکم سیراکوز از او دعوت کند تا برای تربیت جانشینش به آن جا برود. این سفر به علت حوادثی که پیش آمد، برای افلاطون جز رنج و دشواری در پی نداشت و او به آتن بازگشت. وی بعدها سفر دیگری هم به سیراکوز داشت که آن هم بی نتیجه بود.

او از سال 360 ق.م که پایان سفر سومش بود، تا آخر عمر به فعالیت های علمی و فلسفی خود ادامه داد و در سال 348 ق.م درگذشت.

افلاطون پایه گذار و در واقع طلایه دار بسیاری از مباحث عمیق فلسفی است. یکی از متفکران قرن بیستم می گوید: تمام تاریخ فلسفه تا به امروز، چیزی جز حاشیه نویسی بر آثار افلاطون نیست. او در فلسفه که تا آن زمان حول حقیقت واقعی اشیاء می گشت افق های تازه ای گشود و برای اولین بار مباحث گسترده معرفت شناسی را مطرح کرد.

او حکیمی الهی بود و حقیقت چیز ها را ورای ماده و محسوسات و جزئیات می جست و بر همین اساس بود که نظریه خاص خود موسوم به نظریه مثل را طرح نمود.

تفکرات وی، مسیر فلسفه را تعیین کرد و شاگرد بزرگش ارسطو در بستر نظریات او بود که حرکت فلسفی اش را آغاز نمود.

از افلاطون آثار بسیار بر جای مانده است که شامل همه موضوعات مهم فلسفه و علوم انسانی می شود؛ مانند فیزیک، سیاست، اخلاق، منطق، زیبایی شناسی و غیره... .

آثار افلاطون همه در شمار بهترین آثار فلسفی تاریخ هستند. از آن ها می توان به رساله های: تیمائوس، تئتتوس، مهمانی، فیدون و پارمنیدس اشاره کرد. مهم ترین ومشهور ترین اثر او جمهوری نام دارد که جزو ده کتاب برتر تاریخ محسوب می شود.
برای آگاهی از افکار او، بنگرید به:
· آراء و افکار افلاطون
· آثار افلاطون
http://www.daneshnameh.roshd.ir/mavara/mavara-

چگونه سیستم سالم و بدون مشکلی داشته باشیم:

چگونه سیستم سالم و بدون مشکلی داشته باشیم:همه شما شاید تا به حال چندین بار خود اقدام به نصب ویندوز کردید و یا اینکه کیس خود را به یک شرکت خدمات کامپیوتری برده واقدام به تعویض ویندوز خود کرده اید.ایا تا به حال به این موضوع فکر کرده اید که چرا ویندوز از کار می افتد ویا سرعت آن فوق العاده کند می شود و یا اینکه سالی چند بار اقدام به نصب ان می کنید اگر کاربر حرفه ای ویندوز هستید شاید این مقاله بسیار مقدماتی و ابتدائی به نظر برسدولی این حقیقت دارد که اکثر کاربران ویندوز فقط و فقط از ویندوز استفاده می کنند و هیچگاه اقدام به سرویس و یا بررسی ویندوز خود نمی کنند .چندین عامل باعث مشکل در ویندوز می شود که تا حدودی با انها آشنا می شویم.در ابتدا همیشه کاربران اقدام به نصب برنامه های گوناگون به روی سیستم می کنند.همیشه به یاد داشته باشید با نصب یاunistall کردن یک برنامه رجیستر ویندوز تغییر می کند و برنامه نصب شده اقدام به تغییرات دلخواه خود در در رجیستری می کند. رجیستری قلب ویندزو شماست پس باید همیشه سالم باشد .هنگامی که برنامه ای راپاک کردید باز هم کلیدهای ان برنامه در مدخل رجیستری باقی می ماند پس اولین کار محافظت از آن است .برای این کار همیشه یکback up از رجیستری داشته باشید و ره چند وقت یکبار با نرم افزار مفیدی مانند REGISTERY Mechanic اقدام به پاکسازی آن کنید .در مرحله بعد ویروسها می توانندقسمتهای اصلی ویندوز را هدف قرار دهند سپس نرم افزارهای ضد ویروس بهترین پیشنهاد است مانندNortonو یا ... به مرور زمان ممکن است برخی فیلهای ویندوز گم ویا از بین بروندپس گزینه Repairکردن ویندوز می تواند کار گشا باشد.کاربرانی که زیاد بازیهای کامپیوتری بازی می کنند بدانند چون برخی فیلهای بازیها (فایلهایdll;)در پ.شه های ویندوز کوپی می شوند می تونند باعث اخلال در عملکرد سیستم شوند پس به یاد داشته باشید همزمان بازیهای زیادی را در سیستم خود نصب نکنید و اگر این کار را کردید سعی کنید در درایوی که ویندوز در آن نیست اینکار را انجام دهید .بسیاری از مشکلاتی که برای ویندوز پیش می آید به راحتی قابل برطرف شدن است پس نترسید و حدالامکان خود اقدام به تجربه کنید. فراگیری زبان ویندوز بسیار می تواند به شما کمک کند .مسئله مهم دیگر اینکه سعی کنید در پوشه ای که ویندوز را نصب کردید حدالامکان عملیات روزمره مانند کپی کردن فایلها و... را در درایوی غیر از درایو ویندوز انجام دهید وبا درایو وینوز خود (مثلاً درایو:C) کا رنکنید. از بررسی و عملیات روی پوشه های ویندوز در صورتی که اطلاعات علمی و تخصصی کافی نداشته باشید جداً بپرهیزید .هر چند وقت یکبارhistory ویندوز وIE و برنامه های دارای history را بررسی و فایلهای اضافی را پاک کنید در محیط cmdدستورF/CHKDSKرا هر چند وقت یکبار اجرا کنید .همیشه به یاد داشته باشید ویندوز عمر شخصی نداردو نحوه عملکرد ویندوز تا حدود بسیار زیادی بستگی به نحوه استفاده شما از ویندوز دارد .در خود ویندوز گزینه های مهم دیگری بعد از فشردن 8F هنگام boot شدنوجود دارد که شما را از نصب مجدد ویندوز بی نیاز می کند .کار با برنامه های کمکی مانند Tuneup,reg cleaner ,...می توانند بسیار به شما کمک کند. امیدوارم این مقاله توانسته باشد تا حدودی مشکلات را بر طرف کند.

جواد قربانی

اگرازدست درس ومشق خسته شدید

اگرازدست درس ومشق خسته شدید بد نیست سری به سایتهای زیر بزن

http://www.niksalehi.com

http://www.3tareha.com/

http://www.1000toman.com/fun.html

http://www.dardesar.ir/dardesar/

http://www.linkestan.com/

http://uk.news.yahoo.com/hot/office-attachments/

سری به سایتهای زیر بزن اگر بازی خور هستی

www.games.com

www.hotgames.com

www.miniclip.com                      -

- http://www.gamespy.com/                             -

- http://www.gamespot.com/                            -

- http://www.happypenguin.org/news                    -

- http://www.happypuppy.com/                          -

- http://www.dfg.ca.gov/                              -

- http://www.sega.com                                 -

- http://www.gamestudies.org/                         -

- http://www.gamesdomain.co.uk/indexuk.html           -

- http://zone.msn.com/en/root/default.htm             -

- http://shop.game.net/                               

ریاضیات و رانندگان

رانندگانی که به ریاضیات خود مطمئن بودند و در ترافیک همیشگی بزرگراه شماره 101 که به «سیلیکون ولی» منتهی میشود، گیر میکردند، میتوانستند وقت خود را با تامل در بیلبوردی که روی آن یک مسئله ریاضی نوشته شده بود، بگذرانند. کسانی که میتوانستند عدد موردنظر سؤالکننده را دریابند، در واقع مبنای یک الگوریتم طبیعی را مییافتند. تعداد کسانی که روی این معما کار کردند و از عهده حل آن برآمدند، به وبسایتی رهنمون شدند تا مسئله ای دیگر را حل کنند و پس از حل این معما هم، صفحه ای دیگر به روی آنها گشوده میشد که از آنها میخواست تا مشخصات و سوابق کاری خود را ارسال کنند. اگر بیلبوردی میتوانست روح یک شرکت را به تصویر بکشد، همین بیلبورد بود، زیرا آگهی دهنده ناشناس شرکت گوگل بود که محصول اصلی و مهم آن محبوبترین موتور جستجوی اینترنتی در جهان است. با این شوخی جسورانه، با اشتغالات ذهنی ریاضی، سادگی و این اعتقاد مبتکرانه که گوگل منزلگاه نوابغ است، بیلبورد از شرکتی سخن میگفت که فکر میکند جایگاه درست و به حقی را به عنوان رهبر و پیشروی صنعت فناوری به دست آورده است، موقعیتی که در 15 سال گذشته، مایکروسافت اشغال کرده بود.

لحن بیلبورد گوگلی بود، چیزی که کارفرماهای گوگل علاقه دارند، بگویند. سخنگوی شرکت میگوید که این صفت «گوگلی»، جهان وطنی، تواضع، تفاوت و تشخیص متعادلی را به ذهن متبادر میکند. نمایشی مناسب و زیبا از گوگلی بودن «googly–ness» که در سخنرانیهای امسال در لاسوگاس اجرا شد درحالی که روسای دیگر شرکتهای فناوری به جایگاه سخنرانی در میان هیاهوی موسیقی راک و رقص نور وارد میشوند، گوگل کنسرت براندنبورگ شماره سه از باخ را پخش کرد، تا روسای شرکت به جایگاه وارد شوند. بیلبورد از این جهت گوگلی بوده، یعنی مانند صفحه اصلی گوگل، به لحاظ بصری به طور کامل ساده بود چنانکه مراجعه کنندگان را درباره محتوای پیچیده آن به اشتباه میاندازد، یا اینکه، برای بیگانگان "گوگلی بودن"، به معنای آرزویی جسورانه و یک ماموریت است که شما را به پیشرفت جهان و یکی دانستن جهل با فضیلت فرا میخواند، عارضه اصلی این طرز فکر که در بیلبورد نشان داده شده است، بزرگ دانستن ریاضیات است. گوگل پیوسته درحال طرح جناسهای عددی و معماهای ریاضی است. وقتی آنها در سال 2004 اسناد مربوط بازار سهام را پر میکردند، گفتند که آنها میخواهند 828/281/718/2 دلار سود به دست بیاورند که برابر با e میلیارد دلار است.

علاقه به ریاضیات در گوگل، شاید از علاقه موسسان آن سرگئی برلین و لری پیج ناشی میشود. برلین که در روسیه متولد شده است پسر استاد آمار است و مادرش هم برای ناسا کار میکند و والدین لری پیج هر دو معلم رایانه هستند. راز موفقیت گوگل که آن را محبوبترین موتور جستجو در جهان ساخته است، درک این موضوع است که بی نظمی در اینترنت یک نظم ضمنی ریاضی دارد. لری پیج و سرگئی برلین با شمارش، تنظیم و ارزیابی ساختارهای ارتباطی توانستند نتایج جستجو را به هم مربوط و نزدیک کنند، کاری که هیچ موتور جستجوی دیگری نتوانسته بود انجام دهد.

تاکنون آنها این برتری را حفظ کرده اند. دانیل سولیوان، دبیر خبرنامه صنعتی آنلاین، گوگل را در صدر بهترین موتورهای جستجو قرار داده است، پس از گوگل، یاهو (yahoo)، اسک (ASK) و MSN مایکروسافت در رتبه های دوم تا چهارم قرار دارند. تعداد بازدیدکننده های گوگل به طور نسبی هر ماه نسبت به سال گذشته در همان ماه افزایش پیدا میکنند. به استثنای AOL که از ورودی اینترنتی مانند فناوری جستجوی گوگل استفاده میکند، در ماه مارس گوگل میزبان نیمی از کل جستجوگران اینترنتی بوده است، سهم گوگل به استثنای AOL از کل جستجوگران 43 درصد بود.

مهارت و توانایی ریاضی دلیل نیمی از موفقیتهای گوگل است: توانایی تبدیل همه جستجوها به پول. برعکس شرکتهای نرم افزاری مانند مایکروسافت که بخش اعظم درآمد آن از محل لیسانس است، گوگل در وهله اول یک بنگاه تبلیغاتی محسوب میشود. او آگهیهای تبلیغاتی معمولی نمیفروشد. بلکه گوگل یک ژانر تبلیغاتی جدید و کارا به نام "پرداخت به ازای هر کلیک" ابداع کرده است. گوگل یک متن کوچک تبلیغاتی روی صفحات نتایج جستجو قرار داده است، اما آگهی دهندگان فقط زمانی پول برای آن پرداخت میکنند که بازدیدکنندگان و کاربران اینترنتی به طور حتم روی آن متن کلیک کرده باشند و وارد آدرس آنها شده باشند. این سیستم روی صفحات نتایج جستجو تا به حال خوب کار کرده و نیمی از درآمد گوگل را تامین کرده است، زیرا کلمات اصلی کاربران به گوگل اجازه میدهد تا آگهی های مناسب و مربوط به آن را روی صفحه قرار دهد. اما در عین حال این سیستم روی دیگر صفحات وب مانند بلاگها و مقالات روزنامه هم که به عنوان بخشی از شبکه گوگل امضا میشوند، جواب داده است.

مغز جهان

این دو موتور به هم پیوسته، الگوریتمهای جستجو با الگوریتمهای تبلیغاتی، موتوری است که باعث افزایش درآمد (6/1 میلیارد دلار در سال گذشته) و سود آن (5/1 میلیارد دلار) و نیز افزایش سرمایه بازار آن (117 میلیارد دلار) شده است و به همین دلیل است که اولین سرمایه گذار گوگل که موسس مایکروسیستم های سان هم بوده است، تاکنون سهام خود را در گوگل حفظ کرده است.

گوگل از زمان ورود به بازار سهام، محصولات جدید به طور غالب متفاوتی را به این موتورهای دوقلوی خود افزوده است. این شرکت حالا صاحب "پیکاسا" ((Picasa نرم افزاری برای تصحیح عکسهای دیجیتال روی رایانه، اورکات (Orkut) یک شبکه ارتباطی اجتماعی که در برزیل محبوبیت زیادی دارد، بلاگر که به مردم امکان راه اندازی ژورنال آنلاین میدهد است. گوگل همچنین به تازگی نرم افزار مجانی برای ردوبدل کردن پیامهای فوری و تلفن اینترنتی و برای جستجو بر روی دسکتاپ رایانه کاربران، برای پرواز مجازی دور زمین، برای حفظ رایانه در مقابل ویروس و برای ایجاد صفحه اینترنتی ارایه داده است. همچنین گوگل برنامه ایمیل مجانی و تقویم دارد. به تازگی هم شرکتی به نام Writely"" خریداری کرده است که به مردم این امکان را میدهد که "متن" ایجاد کنند و روی اینترنت نگه دارند، درست مانند "Word" مایکروسافت، اما با این تفاوت که شما متون خود را میتوانید در Writely برعکس "Word" روی اینترنت ذخیره کنید. علاوه بر این گوگل درحال اسکن کتابهای کتابخانه های مختلف برای تهیه و راه اندازی کتابخانه آنلاین است.

سانفرانسیسکو و شاید چند شهر بزرگ دیگر گوگل آماده است تا اینترنت Wireless مجانی ارایه دهد. اینها فقط مواردی از یک فهرست بلندبالا از محصولات گوگل است.

اینکه اینها سرگرمیهای دلخواه است، بستگی به نظر شما دارد. برای لریپیج و سرگئی برلین، این محصولات معنای ریاضی دارند و برلین حساب کرده است که مهندسان گوگل باید 70 درصد وقت خود را صرف محصولات اصلی گوگل یعنی موتور "جستجو و تبلیغات" کنند و 20 درصد دیگر وقت خود را صرف محصولات مربوط اما فرعی و 10 درصد دیگر را صرف تفریحات کنند. نتیجه اینکه گروههای کوچک بسیاری بر روی این پروژه ها کار میکنند. مهمترین ماموریت و وظیفه ای که درحال حاضر گوگل برای خود قایل است، "سامان بخشیدن به اطلاعات جهان" یعنی اسکن و فهرست کردن اطلاعات است که اطلاعات آفلاین را آنلاین میسازد.

جهان خارج از گوگل به این موضوع متفاوت نگاه میکند، طرفداران گوگل تصور میکنند شرکتی آمده است تا اینترنت را هرچه کوتاهتر و خلاصه تر کند. با این دیدگاه به نظر میرسد که آنها همزمان روی چند پروژه کار میکنند و هر محصول جدیدی صرفنظر از اینکه چه اندازه بی اهمیت است، مرحله و گامی کوچک به سوی تحول نهایی جهان محسوب و از آن استقبال میشود.

حداقل چیزی که اتفاق میافتد رایانه ای کردن داده های رایانه های شخصی و اتصال آنها به سرورهای گوگل است، نام دیگر این سناریو "GDrive" و یا شبکه گوگل "Google grid" است که شرکتی مدعی است دارد بر روی آن کار میکند و به معنای انبار ذخیره بزرگ و به احتمال قوی با امکان دسترسی مجانی به اینترنت است. انبار ذخیره مجانی تهدیدی برای مایکروسافت به شمار میرود زیرا نرم افزارش به جای اینترنت روی رایانه های شخصی نفوذ و تسلط دارد و دستیابی جهانی به اینترنت، ارایه دهندگان سرویس دستیابی به اینترنت را مورد تهدید قرار میدهد.

و حداکثر آنکه این تحول، اندکی فراتر میرود. جورج وایسون که زمانی را در گوگل به سر برده است، معتقد است که شرکت در نهایت علاقه دارد تا همه سیناپس های دیجیتال که به وسیله کاربران ایجاد شده است را به آنچه "مغز جهان" نامیده میشود، متصل کند. وی فکر میکند که گوگل در آرزوی تحقق این رویای بزرگ یعنی خلق "هوش مصنوعی" است. عبور از آنچه "آزمایش تورینگ" (Turing text) نامیده میشود و به وسیله آلن تورینگ، ریاضیدان بریتانیایی انجام شد برای اینکه معلوم شود آیا یک ماشین میتواند فکر کند یا خیر، مهمترین و بزرگترین پاداش گوگل، لری پیج و سرگئی برلین خواهد بود.
http://www.itnewsway.com

 

 

موتور جستجوی گوگل

موتور جستجوی اینترنتی گوگل ‬هفت سالگی خود را با تغییر لوگوی صفحه اول این سایت جشن گرفت.

در لوگوی جدید گوگل، حرف (L) ‬در كلمه ‪ Google‬به شكل عدد انگلیسی هفت ‬درآمده و در پایین كلمه Google هفت قطعه كیك تولد به شكل چشم دیده میشود. گوگل كه در زمان حاضر به عنوان محبوبترین موتور جستجوی اینترنتی در جهان شناخته شده است، فعالیت خود را از سپتامبر سال 1998 ‬با هدف جمعآوری و سازماندهی اطلاعات دنیا و در دسترس قرار دادن آنها شروع كرد.

موتور جستجوی گوگل در سالهای گذشته نوارهای ابزار و امكانات مختلفی را برای جستجوی بهتر و استفاده از اطلاعات موجود در شبكه اینترنت به كاربران ارایه كرده است. از جمله امكانات این سایت، جستجو در وب سایتها، تصاویر، اخبار، گروهها، فروشگاهها و وبلاگها است.

گوگل كه خدمات جستجوی خود را به بیش از 100 ‬زبان زنده دنیا ارایه میدهد در چند ماه اخیر خدماتی مانند مسنجر، كتابخانه دیجیتالی و مشاهده تصاویر ماهوارهای را نیز برای كاربران خود فراهم كرده است.

بیشترین درآمد گوگل در زمان حاضر از محل آگهیهای متنی آن به دست میآید به طوریكه تاكنون میزان سود خالص این موتور جستجو حدود 400 ‬میلیون دلار برآورد شده است.

موتور جستجوی گوگل در سال 1998 ‬توسط دو دانشجوی رشته ریاضی دانشگاه "استنفورد" آمریكا راهاندازی شد و امروزه به ثروت هنگفتی دست یافته است.



http://www.winbeta.net/comments.php

مهارت جستجو

در این مقاله با ۲۵ نکته کاربردی برای استفاده بهتر از موتور جستجوی گوگل آشنا می شوید.

1 – همه چیز در نحوه نوشتن: با اطلاع از چگونگی نوشتن عبارات جستجو در موتورهای جستجو، میتوانید اطلاعات مورد نیازتان را به راحتی پیدا کنید. به عنوان مثال دستور <کلمه مورد نظر: Inurl> باعث میشود تا موتور جستجوی گوگل، همه صفحاتی که در آدرس url آنها، کلمه مورد نظر وجود داشته باشد را برایتان فهرست کند.

 
2 - نوار ابزار گوگل: با اضافه کردن نوار ابزار گوگل به مرورگرتان، از این پس میتوانید کار جستجو را با سرعت و راحتی بیشتری انجام دهید. یکی دیگر از امکانات این نوار ابزار، جلوگیری از نمایش پنجرههای تبلیغاتی است. برای دریافت این برنامه و کسب اطلاعات بیشتر به نشانی  toolbar.google.com  مراجعه کنید.

 
3 - چه کسی به سایت شما لینک داده است : بسیاری از مدیران سایتها علاقه مندند بدانند چه کسانی (از سایت خود) به سایت آنها لینک داده است. گوگل به این سوال پاسخ میدهد. میتوانید در قسمت جستجو، عبارت <نشانی سایت:link> را وارد کرده و کلید Enter را بزنید. نتیجه این درخواست، فهرست سایتهایی است که به سایت شما لینک داده اند.

 
4 - کاربردهای تجاری: دو موتور جستجو فرعی گوگل که به تازگی راه اندازی شده اند و هنوز واژه کالاهای تجاری، مورد استفاده قرار میگیرند. موتور froogle.google.com فهرست محصولات فروشگاههای online را تهیه میکند و موتور calatogs.google.com برای نمایش و درخواست کاتالوگ محصولات به کار میرود.

 

 5 - نگاهی به آینده :مدیران گوگل همیشه نیم نگاهی به آینده دارند. اگر میخواهید بدانید چه در سر آنها میگذرد و قرار است در آینده چه کارهایی انجام دهند، بهتر است سری به آزمایشگاه آنها بزنید و خود از نزدیک با خدمات و محصولات آتی گوگل آشنا شوید. آدرس آزمایشگاه گوگل labsl.google.com/gvs.html میباشد.

6 - نتایج مطلوبتر: در اغلب موارد، زمانی که جستجویی را با گوگل انجام میدهید، نتیجه آن هزاران سایت و وبلاگ و نشانی میباشد که در واقع بسیاری از آنها کاربرد چندانی ندارند و با موضوع موردنظرتان هماهنگ نیستند. یکی از روشهای مؤثر در کاهش حجم نتایج جستجو، تعیین بازه های تاریخی است. مثلاً زمانی که بازه ای را بین سالهای 2002 تا 2004 تعریف میکنید، گوگل با تبعیت از آن، فقط آن دسته از صفحاتی که در بازه مذکور ایجاد یا روزآمد شده اند را برایتان فهرست میکند (برای تعریف بازه های تاریخی به گزینه <جستجوی پیشرفته> مراجعه کنید).

 
7 - فقط صفحات جدید: جستجو بدون ذکر تاریخ، نتایج بیشماری در پی دارد. انبوه نتایج، نه تنها به یافتن مطلب موردنظرتان کمکی نمیکند، بلکه موجب سردرگمیتان نیز میشود. علاوه براین اگر بعد از یک بررسی طولانی بین نتایج جستجو، به اطلاعات موردنظرتان رسیدید و متوجه قدیمی بودن آنها شدید، چطور؟ اگر به دنبال اطلاعات جدید و روزآمد هستید، در قسمت جستجوی پیشرفته، عبارات <3 ماه>، <6 ماه> و حتی <یکسال> را در مقابل گزینه Date وارد کنید تا گوگل بسته به تاریخ ذکر شده، فقط فهرست صفحات جدید را برایتان نمایش دهد. مثلاً اگر عبارت <3 ماه> را انتخاب کنید، گوگل تمامی صفحاتی که در سه ماه گذشته ایجاد یا بروز شده اند را جستجو و آنهایی که با موضوع موردنظرتان منطبق هستند را نمایش میدهد.

 
8 - مستثنی کردن کلمات: با مستثنی کردن کلمات، علاوه بر کاهش حجم نتایج جستجو، میتوان به اطلاعات موردنظر نزدیکتر شد. با گذاشتن علامت <-> قبل از کلمه دلخواه، گوگل آن کلمه را استثنا قلمداد کرده و از نمایش صفحاتی که حاوی چنین کلمه ای باشند، پرهیز میکند. مثلاً نتیجه عبارت ، همه صفحاتی که مربوط به ایران هستند و از تهران نامی نبرده اند را شامل میشود.

9- Wildcardها: زمانی که به طور کامل از کلمات موضوع مورد جستجو آگاهی ندارید، بهتر است از کاراکتر کمکی ستاره <*> استفاده کنید. کاراکتر <*> معنی <هرچیز> میدهد. مثلاً عبارت میتواند نتایجی نظیر ، و یا نتایجی از این دست را حاصل شود.

10 - عناوین صفحات :معمولاً همه صفحات وب، عنوان دارند. گاهی اوقات استفاده از این عناوین، به شما در پیدا کردن مطالب مورد نیازتان کمک شایانی میکند. مثلاً عبارت <کلمه مورد نظر: intitle>، گوگل را بر آن میدارد تا فقط عناوین صفحات را برای یافتن کلمه ذکر شده، جستجو کند.

11 - شرکت در گروههای خبری: اینترنت فراتر از ایمیل و صفحات وب است. به عنوان مثال گروههای خبری (News group) یکی دیگر از خدماتی است که از طریق اینترنت ارایه میشود. گروههای خبری گوگل، گروههای معروف و معتبری هستند که شرکت در آنها، به نوبه خود، کار لذتبخشی است. آدرس گروههای خبری گوگل از این قرار است: groups.google.com

12 - جستجوی خودکار: جستجو در اینترنت، قصه سوزن و انبار کاه است. گاهی اوقات ممکن است علیرغم صرف وقت زیاد، باز هم به نتیجه دلخواه نرسید. بنابراین هر ابزاری که در این پروسه، از اتلاف وقت جلوگیری کند، بسیار باارزش است. یکی از این ابزارها، <پیغام دهنده> گوگل نام دارد. این ابزار با دریافت آدرس ایمیل و عبارت مورد جستجو، به طور خودکار و روزانه، جستجویی را براساس عبارت دریافتی ترتیب داده و هر زمان که اطلاعات جدیدی را یافت نماید، آدرس آن را برایتان ایمیل میکند. آدرس پیغامدهنده گوگل به این ترتیب است: www.googlealert.com

13 - جستجوگر اخبار: این ابزار نیز همانند پیغام دهنده گوگل، مشخصات اخبار موردنظر را به همراه آدرس ایمیل دریافت کرده و روزانه (بنا به درخواست کاربر، قابل تنظیم است). براساس عبارت دریافتی، جستجویی را در سایتهای خبری ترتیب میدهد و در صورت یافتن اطلاعات مناسب، آن را برایتان ایمیل میکند. آدرس این ابزار www.google.com/newsalerts است.

14 – ماشین حساب گوگل: گوگل برای حل معادلات ریاضی هم، ابزاری دارد که بسیار سریع و با دقت عمل میکند. این ابزار علاوه بر حل معادلات ریاضی، قابلیت تبدیل انواع واحدها به یکدیگر را نیز دارد. برای آشنایی بیشتر با این ابزار کارآمد به آدرس زیر مراجعه کنید: www.google.com/help/features.htm#calculator

15 - معنی کلمات: اگر معنی یا بهتر بگوییم، تعریف کلمه ای را نمیدانید، در کادر جستجو <کلمه موردنظر: define> را نوشته و کلیدEnter را بزنید. در جواب این جستجو، علاوه بر تعریف کلمه، لینکی نیز نمایش داده میشود که با کلیک روی آن، به جزییات بیشتری میرسید.

16 - ترجمه کنید:در حال حاضر، ماشین ترجمه گوگل میتواند انگلیسی را به 5 زبان زنده دنیا ترجمه کند (امکان ترجمه بالعکس نیز وجود دارد). برای استفاده از این مترجم ماشینی به آدرس

 www.google.com/lauguage-tools بروید.

 
17 - تصویریاب :من شخصاً همیشه گوگل را به خاطر ابزار تصویریابش ستوده ام. این ابزار با دریافت کلمه یا عبارتی، تصاویر موجود روی اینترنت را جستجو کرده و در نهایت آنهایی را که با عبارت دریافتی منطبق هستند، فهرست میکند. برای استفاده از این ابزار به آدرس www.google.com/imghp مراجعه نمایید.

 
18 - پرسش و پاسخ: تحقیق و جمع آوری مطالب از اینترنت، کار وقتگیری است. اگر برای انجام اینکار وقت کافی در اختیار ندارید. سری به آدرس answers.google.com/answers بزنید و با مطرح کردن سوالاتتان و بررسی جوابها، سریعتر به هدفتان برسید.

19 - نمایش پنجره تنظیمات: گوگل به شما این امکان را میدهد تا نحوه نمایش نتایج را مطابق میلتان تنظیم کنید. به عنوان مثال با مراجعه به آدرس www.google.com/preferences میتوانید تعداد نمایش نتایج در هر صفحه را تعیین نمایید. علاوه براین در قسمت تنظیمات امکانات دیگری نظیر Safe Searching نیز وجود دارد. با فعال کردن این گزینه، گوگل از نمایش سایتهایی که به هر دلیلی غیرمجاز هستند، پرهیز میکند.

20 - آمار استفاده از گوگل: در سایت www.google.com/press/zeitgeist.html آمار جهانی استفاده از گوگل موجود است. در این سایت جزییاتی از چگونگی استفاده ملل مختلف از گوگل و الگوهای جستجوی آنها وجود دارد.

21 - جستجو در دسته بندیها: علاوه بر جستجوی کلی وب، گوگل امکان جستجو در دسته بندیها (Categories) را نیز میدهد. به عنوان مثال برای یافتن اطلاعاتی درباره هنر، تجارت، ورزش و ... میتوانید ضمن مراجعه به نشانی   www.google.com/dirhp جستجویی را در دسته بندیهای گوگل ترتیب بدهید و سریعتر به هدفتان برسید.

 
22 - برای بلاگرها وبلاگ داشته باشیم یا نه؟ ایده داشتن یک وبلاگ شخصی، بسیار جالب است و اینکه با در اختیار داشتن یک وبلاگ شخصی حرف دلمان را به گوش جهانیان برسانیم، فکر بسیارخوبی است. برای ساخت یک وبلاگ شخصی، به آدرس www.blogger.com/start مراجعه نمایید. این سایت متعلق به گوگل است.

 
23 - جستجوی داخل فایلها : با کمک گوگل میتوان داخل فایلهای مشخصی را برای یافتن کلمه ای دلخواه جستجو کرد. مثلاً عبارت:گوگل را برآن میدارد تا تمامی فایلهای doc (مربوط به برنامه Microsoft word) را به منظور یافتن واژهی Iran جستجو کرده و آنهایی که دارای چنین کلمه ای هستند را فهرست کند.

 
24 - کلمات عمومی: برخی کلمات عمومی نظیر the ،to ،at و غیره، زمانی که در عبارت مورد جستجو ذکر میشوند، توسط گوگل نادیده انگاشته میشوند و تاثیری در نتیجه ندارند. حال اگر میخواهید چنین کلماتی در نتیجه جستجو موثر باشند کافی است یک علامت <+> در مقابل آنها بگذارید.

25 - موتورهای جستجوی تخصصی: با این ترفند میتوانید ضمن معرفی منابع موردنظرتان به گوگل، از آن بخواهید که نتایج جستجو را فقط از همان منابع بیاورید. مثلاً برای جستجو در سایت مایکروسافت به روش زیر عمل میشود: www.google.com/microsoft

 

 

ضرورت استفاده از کامپیوتر برای دانشجویان مخصوصاً دانشجویان ریاضی:

استفاده از کامپیوتر در دنیای امروزی دیگر امری ضروری ودر عین حال عادی شده است. استفاده از این ماشین همه کاره میتواند بسیار به ما کمک کند. در دنیائی که دیگر محاسبات در حد میلیارد بر ثانیه انجام می گردداستفاده از کامپیوتر برای دانشجویان باید امری ضروری باشد با استفاده از این وسیله و نرم افزارهای مورد استفاده دیگر لازم نیست برای رسم یک منحنی پیچیده دیگر از کاغذ استفاده کنیم بلکه با وارد کردن مشخصات می توان خروجی مناسب را دریافت کرئ و سپس آنالیز دقیقی بر آن نمود. شاید شما به این فکر بیافتید که این کار برای دانشجوی ریاضی شاید کمی تنبلی باشد ولی جواب این نیست بلکه استفاده از این وسیله باعث سرعت بخشیدن برای رسیدن به جواب دلخواه است در حالی که بررسی و تحلیل درست ان فقط از عهده مغز بر میآید وقتی ابر کامپیو تر ها ی جهان که سرعت آنها گاهی به  میلیارد هامحاسبه در ثانیه می رسد نمی توانند تفکر کنند و راه حل درست را ارائه دهند مگر آن که مغز آدمی الگوریتم آن را پیدا کرده باشد . پس همین حالا دست به کار شده و یک نرم افزار ریاضی را امتحان کنید.

جواد قربانی جم

چگونه از کامپیوتر خود در شبکه محافظت کنیم

 

در این لحظه که شما مشغول خواندن این وبلاگ هستید یا مشغول مرور صفحات وب هستید آیا کامپیوتر شما در این دریای اطلاعات دارای محافظ است؟

در جهان وب همیشه کامپیوتر شما در معرض خطرهای گوناگونی از قبیل ،ویروس ها،جاسوس افزارها،تروجا ن ها،دیالرها ( Dialer)

و ... است که اگر کامپیوتر شما دارای حفاظ مناسبی نباشد می تواند صدمات جبران ناپذیری را به شما وارد بیاورد از قبیل دزدیده شدن اطلاعات ،passwordها شماره های کارتهای اعتباری و... است.

در این جا نمی خواهیم از چگونگی کار یک آنتی ویروس یاAntispy wareآشنا شویم بلکه به معرفی یک حفاظ برای شما می پردازیم.

شرکتهای زیادی برنامه های مختلف را نوشته اند از قبیل مک آفی ،نورتون،Zone AlARM,Bitde fender،پاندا،spy Bootو

کسپرسکی و... . یکی از نکات مهم یک آنتی ویروس یا نرم افزار امنیتی قابلیتUpdate شدن آن است . یکی از این برنامه ها که توسط خود نویسنده استفاده و امتحان شده است نرم افزارZONEALARM SECURITY SUITاست. این نرم افزار در واقع یک برنامه کامل آنتی ویروس ، آنتی اسپای وار و Firewall است که شما را از بقیه نرم افزارها بی نیاز می کند .از ویژگیهای خوب این نرم افزار قابلیت Updateشدن سریع آن است fire wallآن شما را در مقابل هک شدن و خروج اطلاعات شما محافظت و به شما هشدار می دهد.

البته این نکته را در نظر بگیرید که هیچ نرم افزار حفاظتی نمی تواند شما رادر مقابل همه خطرها محافظت کند ولی تا حدودی امنیت شما را تضمین می کند . این نرم افزار را میتوانید به صورت قفل شکسته از فروشگا ههای نرم افزار تهیه کنید . نسخه اصلی این نرم افزار با قیمت چندین برابر!! نیز در نمایندگیهای فروش این شرکت موجود است . توضیحات این مقاله بسیار کلی و عمومی بود. پس خود اقدام به نصب و استفاده از این نرم افزار نمائید.

دانش علی

روزی شخصی به حضور امام علی (ع) آمد گفت :عددی را به من بگو که بر تمامی اعداد 1.2.3.4.5.6.7.8.9.10 قابل تقسیم باشد بدون آنکه هیچ کسری بیاورد .حضرت فرمود :روزهای هفته را در تعداد روزهای سال ضرب کن عدد مورد نظر به دست می آید .
عدادهای خواسته شده 7و356 بود که 356*7 =2520 که بر همه اعداد 1 تا 10 قابل تقسیم است.



برگرفته از 110 داستان جوانی علی (ع)
ناشر:انتشارات صدا وسیما (سروش)

اعداد شیطانی

عدد شیطان
اگر شما به دقت فیلمهایی با مضامین شیطانی و مرگ و روح را مشاهده کرده باشید مطمئنا به کارگیری عدد ۶۶۶ در اینگونه فیلمها شما را متعجب میکند. این موضوع ما را بر آن داشت تا این پست را اختصاص دهیم به کاوش در اسرار ۶۶۶.
۶۶۶ را علامت ابلیس نامیده اند و این شهرت را از کتاب وحی(فصل ۱۳، شعر ۱۸، برای کامل بودن) به دست آورده است. مشخصات جالبش همواره مورد توجه ریاضیدانان بوده است. اکنون به طور خلاصه چند ویژگی ریاضیاتی عدد ۶۶۶ را بیان میکنیم.
عدد ۶۶۶ به سادگی از جمع و تفریق توانهای ششم سه عدد آغازین به دست می آید.
۶۶۶=۱۶-۲۶+۳۶
همچنین این عدد برابر است با مجموع ارقام خود باضافه جمع توانهای سوم ارقامش.
۶۶۶=۶+۶+۶+۶۳+۶۳+۶۳
تنها پنج عدد صحیح مثبت با چنین خاصیتی وجود دارند. آنها را پیدا کنید.
جمع توانهای دوم ۷ عدد اول برابر است با ۶۶۶.
۶۶۶=۲۲+۳۲+۵۲+۷۲+۱۱۲+۱۳۲+۱۷۲
جمع ۱۴۴ رقم ابتدایی عدد پی برابر ۶۶۶ است. نکته جالب اینجاست که
۱۴۴=(۶+۶)×(۶+۶)
۶۶۶ یکی از دو عدد صحیحی میباشد که برابر مجموع توانهای سوم از ارقام توان دوم خویش باضافه مجموع ارقام توان سومش است. یعنی:
۶۶۶۲=۴۴۳۵۵۶
۶۶۶۳=۲۹۵۴۰۸۲۹۶
۶۶۶=(۴۳+۴۳+۳۳+۵۳+۵۳+۶۳)+(۲+۹+۵+۴+۰+۸+۲+۹+۶)
۲۵۸۳ عدد دیگریست که دارای این خاصیت میباشد.
مجموع ۶۶۶ عدد اول حاوی عدد ۶۶ میباشد.
۲+۳+۵+۷+۱۱+...+۴۹۶۹+۴۹۷۳=۱۵۳۳۱۵۷=۲۳×۶۶۶۵۹
دقیقا دو راه برای قرار دادن علامت "+" در رشته ۱۲۳۴۵۶۷۸۹ داریم تا ۶۶۶ حاصل شود در صورتیکه تنها یک راه برای رشته ۹۸۷۶۵۴۳۲۱ وجود دارد.
۶۶۶=۱+۲+۳+۴+۵۶۷+۸۹
=۱۲۳+۴۵۶+۷۸+۹
۶۶۶=۹+۸۷+۶+۵۴۳+۲۱
۶۶۶ مقسوم علیه ۱۲۳۴۵۶۷۸۹+۹۸۷۶۵۴۳۲۱ میباشد.
عدد اسمیت عدد صحیحی است که مجموع ارقامش برابر است با مجموع ارقام عوامل اول خودش. ۶۶۶ یک عدد اسمیت است. زیرا:
۶۶۶=۲×۳×۳×۳۷
۶+۶+۶=۲+۳+۳+۳+۷
تابع (Phi(n در نظریه اعداد عبارت است از تعداد اعداد کوچکتر از n که نسبت به n اولند. قابل توجه است که:
Phi(۶۶۶)=۶×۶×۶
منبع : اینترنت

چگونه بهتر جستجو کنیم

چگو نه در جستجوی اطلا عات موفق باشیم؟

در دنیای امروز که عصر اطلاعات نامیده می شود پیدا کردن اطلا عات مورد نظر خود ، یک هنر محسوب

می شود . در دنیایweb که بالغ بر چندین میلیارد صفحه اطلا عات است پیدا کردن مقاله ،عکس یا هر نوع اطلا عات راجع به یک موضوع خاص کار چندان مشکلی به نظر نمی آید ولی پیدا کردن آن چیزی که دقیقا " مورد نظر ماست گاهی مواقع مشکل به نظر می آید مثلا" شما درباره مبحثی<دتر مینان> دنبال مقاله یا اطلا عات می گردید ممکن است به چندین صفحه اطلا عات دستیابی داشته باشید ولی دقیقا" آنچه را که شما می خواهید ، در آنها نیست یا پیدا کردن آن مشکل است به همین منظور در دنیای web از موتور های جستجو می کنیم که از متداول ترین آنها می توان به Google ، Yahoo، 9A، TRUVEO، altavista ، mamma و غیره استفاده کرد . استفاده از این موتور ها ی جستجو نیز گاهی مواقع نیاز مند رعایت یکسری قواعد خاص است که چند مورد از آنها را بررسی می کنیم . مثلا" در موتور جستجوی Google و غالب موتور های جستجو می توان از نشانگر هایی مانند AND ، OR ، NOT استفاده کرد مثلا" اگر اطلا عاتی راجع به معادلات بدون روش حل می توان از ( Not solve) استفاده کرد در ضمن علامتهایی مثل "+" ، "-" ، ( ) می توان در این موتور ها استفاده کرد حال آنکه کدام مورد بهترین نتایج را دارد احتیا ج به تمرین و امتحان کردن دارد و هر کسی با توجه به سلیقه خود می تواند بهترین نتایج را بدست آورد. در ضمن در همین موتور ها می توان از تصاویر یا کلیپ های موجود و index شده در اینتر نت استفاده کرد از جمله از خدمات Google. Video برای پیدا کردن کلیپ ها راجع به یک موضوع خاص می توان استفاده کرد .
اگر در روند جستجوی اطلا عات ، هدف مورد نظر خود طبقه بندی کنیم سریعتر به نتایج بهتر می رسیم مثلا" مبحث نور به شاخه فیزیک بر می گردد و می توانیم از عبارت ( optic) physics استفاده کنیم . طبقه بندی باعث فر مو لیته شدن روند جستجوی اطلاعات و هوشمندانه عمل کردن است. با این حال هنوز بهترین موتور های جستجوی دنیا نیز نمی توانند به طور کامل ، به هدف خود به پیدا کردن موضوعی خاص برساند .
دانشمندان ژا پنی مشغول کا ر بر روی یک موتور جستجوی هوشمند هستند که کمترین خطا را در روند پیدا کردن اطلاعات داشته باشیم. به نظر من کار بر روی موتور های جستجو برای دانشجویان ( مخصو صا" کامپیوتر ، و ریاضی) می تواند یک پروژه بزرگ دانشگاهی باشد.همیشه به یاد داشته باشید که عصر امروز عصر جستجو و پیداکردن اطلاعات است به یاد داشته باشید همیشه جوینده یابنده است.

دانلود نرم افزار

اگر علاقمند به استفاده از نرم افزار های ریاضی هستید می توانید به این سایت مراجعه کنید .

---

Graphcalc 4.0.1
Size:842 k
توضیحات: برنا مه ای که به شماامکان طراحی ،نمایش گراف ،معادلات دو بعدی و سه بعدی را می دهد.
شما می توانید ویرایش و نمایش دهیدگرافها را و در 6 جهت دایره ای تجزیه کنید .با مهارت به نشانه گذاری و آنالیز برنامه رسم شده بپردازید.

---

Flashcards 2.4
Size:1800 k
برنامه ای ساده که شامل جمع،تفریق،ضرب،تقسیم است . شما می توانید هر کدام از چهار عمل را با هم ادغام کرده و تایمر در 4 دقیقه مهلت پاسخ را به شما میدهد . این برنامه برای سطوح پائین مناسب تر است.

---

Q_B Math v:2.0

Size:1.500 k
برنامه MATH- QBبه راحتی درWindows اجرا شده و به شما اجازه می دهد که چهار عمل را با عملیات جذابی آزمایش کنید . 5 معما در این برنامه است که برای آموزش بسیار مناسب است.

---

mathemagic
Size:2,590 k
برنامه ای برای معماها و بازیهای ریاضی

---

 برنامه های فوق از سایت     www.teach-nology.com/downloads/math  قابل دریافت است.


Multi Tab 2.1
Size:322 k
برنامه ای فوق العاده ساده برای آموزش ریاضی

---

Find gragh 1.400
Size:2080 k
برنامه ای برای طراحی ،مقیاس منحنیها برای مهندسین

يک نرم افزار جامع گرافيکی با امکانات گسترده برای نمايش داده ها بصورت نمودارو ويرايش آنهاست . با اين نرم افزار قادر خواهيد بود بدون مراجعه به کتابهای آماری و جبر و انتگرال ، باسرعت و راحتی هر چه تمامتر به تجزيه و تحليل اطلاعات پرداخته

و آنها را بصورت نمودار نمايش دهيد . FindGraph دارای 10 نوع محاسبه کلی بوده که تعدادی از آنها به اين شرح است :
Linear Regression, Logistic Functions, Fourier approximation, Neural Networks, plus و ... اين نرم افزار نقشه ها ، طرحها و داده هاي شما را بصورت مختصات X و Y درآورده و در ضمن دارای 120 فرمول صنعتی بوده که برای انجام محاسبات کاربرد فراوانی دارد . از ديگر ويژگيهای اين نرم افزار قدرتمند ميتوان به موارد زير اشاره نمود :
دارا بودن بيش از 200 توابع دو بعدی در بانک اطلاعاتی برنامه ؛ دارای امکانات حساب ديفرانسيل و انتگرال جبر و آناليز ؛ انتقال نقشه و نمودارها از محيط برنامه به محيط برنامه هائی از قبيل Word ، Excel، drawing programs

 

FindGraph نرم افزاری است که همه ، خصوصا مهندسين ، دانشجويان و ... ميتوانند از آن بهره برداری کامل نمايند .

آدرس کرک برنامه:

www.crackzplanet.com/get_61536_FindGraph.v1.460_crack.html

---

ESBPDF Analysis 2.0.0
Size:2564 k
جهت توزیعات احتمال به همراه راهنما

---

Alans MATH 2.5
Size:406 kB
برنامه ای برای ساخت و آموزش مفاهیم پایه علم حساب




** Universal scientific calcultor 3
ماشین حساب قدرتمند ،شامل بسیاری از توابع ریاضی ،چارت ها و بازیهای جالب ریاضی

Algebra-one on one4.0
Size:874 kB
برنامه ای برای آموزش قدم به قدم ریاضیات و جبر در محیطی جذاب
. قابل دریافت است www. Sofotex.comبرنا مه های فوق از سایت



Karnaugh Minimizer 1.4
توضیحات :برنامه کمکی برای جبربولی
Size:3405 k

---

::انتگرال گیری به روش اینترنتی!!!::

 

این یه وبسایتی که در زیر شاخه ی وب سایت جهان ریاضیات (MathWorld) قرار داره. در این وبسایت به راحتی می تونید با رعایت قوانین تایپ ریاضی تمام توابع چه قطبی و چه معمولی رو انتگرالگیری کنین البته به صورت نامعین. در ضمن این وب سایت به صورت randoom نیز توابعی رو داره که شما می تونین از اونها هم استفاده کنین.

آدرس وب سایت: http://integrals.wolfram.com 

---

Calc 3D Pro 2.0.6 

مجموعه ای از ابزارهای ریاضی برای دبیرستان و دانشگاه
Size:4233 k

---

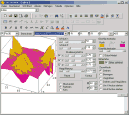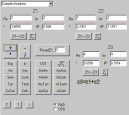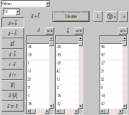
Graphsight 2.0
برنامه ای جامع برای ریاضی دو بعدی و ابزارهای ساده و قابل فهم. این برنامه می تواند خروجی را با فرمت ذخیره کند.XML
Size:741 kB

Math Worm 1.0
معمای ریاضی برای جهت یابی مسیرهای پر پیچ و خم و سوالات چرخشی
Size:1840 kB

برنامه های بالا از سایت www.sofotex.com   قابل دانلود است.

---

::Agate MathGraph ::

برنامه ای است برای جستجو و بررسی توابعی از نوع (y=f(x . کارکرد اين برنامه به دو صورت است : ساختار گرافيکی و محاسبات رياضی . اين نرم افزار دارای پارامترهايی برای اصلاح و تنظيم سطوح گرافيکی می باشد . کليه سطوح گرافيکی قابل ذخيره کردن با فرمت BMP, JPG or GIF هستن . همچنين اين برنامه قادره روشهای محاسبات بکار رفته را بنمايش در بياره . از ويژگيهای اين نرم افزار ميتوان به موارد زير اشاره نمود :
دستورالعملهای نامحدود محاسباتی ؛ پيدا نمودن ريشه معادلات f(x)=0 با فواصل داده شده ؛ ساخت گرافيکی توابع ؛ تحليل مشتقی از محاسبات داده شده و ساخت گرافيکی آن ؛ ساخت گرافيکی خط مماس و نقاط عادی ؛ محاسبه انتگرال و نوسان و پراکندگی توابع ؛ کارکرد آسان و داشتن محيط کاربری دوستانه و ...سازگار با تمامی ويندوزها .

>> دانلود کنید با حجمی معادل ۹۵۰ کیلوبایت 

شماره ی سریال:
Name: LUCiD
Serial: cxv5B5OnxUlgAPbr0Eror6NZfAiZBUCwHgSpByGee
0UzuqePLO6lrQJc2p8KaDaMpVloDqxkcQu3wNbtC6
so8rr6IL9j5o7HuTX4iqk8w6PVU7GSTvq41T16lH2xu
UeiPEp7ckwFAnXVUVs3I1ST9ZuYV8hURb97WH2eJ
BZHGyDcOfI6VsHjwtFqNZcMWKSwOTfPCx3VFJYm
uYZ3yVpk68EK6alAAmiIL1wGZSWkw7O4Kj1TAV5Vr
Lpj4bjWMoebyBveIrpFAWjGQTNiqmD62jEwgjFH02
kTyx1iRdUHotlgAPbr0Eror6NZfAiZBUCwHgSpByG
ee0UzuqePLO6lrQJW

برگرفته از وبلاگ ریاضیات زیبا

---

::تایپ متن با علائم رياضی ::

تایپيست ها و خيلی از برنامه نويسان در هنگام تایپ متنی با علائم رياضی روبرو شدند که در برنامه ای مثل Microsoft Word آن علائم وجود نداشته است.
Design Scienceکمپانی هست که اين مشکل را با نرم افزار Math Type حل نموده است.
Featureهای نرم افزار را ببينيد که حتماً اين برنامه به کار شما هم می آيد.

- امکان تایپ کلیه ی علایم ریاضی اعم از علایم سریها/دنباله ها/مشتق/انتگرال و خیلی چیزهای دیگه.

۲- امکان تایپ فارسی اعداد(که این امکان در ورد وجود ندارد)

۳- امکان کپی برداری از یک فرمول تایپ شده و انتقال آن به نرم افزار هایی نظیر ورد / فتوشاپ

۴- ویرایش مستقیم فرمول از طریق ورد

و...

این نرم افزار رو می تونین در اینجا دانلود نمایید با حجمی معادل ۴.۳۱ مگابایت

کرک: MTWE521-828212-F13UL

---

::نرم افزاری برای ریاضی دانان::

نرم افزار Maple 10 یکی از معروفترین بسته ها برای حل مسائل ریاضی و ساخت برنامه های کاربردی در این زمینه است. شرکت سازنده این نرم افزار با سابقه ای بالغ بر 25 سال، دقیقا نیازها و امکانات مورد نیاز ریاضی دانان خود را به خوبی می داند.
با این نرم افراد علاوه بر انجام انواع محاسبات ریاضی، می تواند اسناد قابل اجرائی بسازد تا نتیجه یک عملیات ریاضی و هم چنین روش آنالیز و راه حل را نمایش دهد. به اسناد ریاضی می توان انواع نمودارها، توضیحات و دکمه ها و . . را اضافه کرد.
نسخه جدید این نرم افزار در این زمینه ها بهبود یافته است: رسم جداول اعداد، محاسبات آماری، حل معادلات دیفرانسیل، بهینه سازی، پردازش تصویر و صدا و . . . .
نمونه ای از کاربردهای Maple در سایت شرکت سازنده موجود است و قابل دانلود می باشند.
www.maplesoft.com
اسیلاتور فاصله های مونیک، طراحی فیلتر دیجیتال، موتور CD، روبروت متحرک و . . .
این نرم افزار به تمام دانشجویان تمامی رشته های مهندسی که با ریاضیات و شبیه سازی سرو کار دارند، توصیه می شود.

---

:: DeskCalc 3.4.0 ماشین حسابی قدرتمند با توانایی های گوناگون ::

ماشین حساب ویندوز با وجود مفید بودن بسیار و تمامی توانایی های مختلف , به عنوان یک ماشین حساب تخصصی و مهدنسی قدرتمند نمی تواند مورد استفاده قرار گیرد . بنا براین وجود یک مشاین حساب تخصصی تر و حرفه ای تر برای برخی افراد نیازی ضروریست .

DeskCalc نام ماشین حسابی قدرتمند از شرکت PmaSoft است که به توسط آن شما قادر به انحام محاسبات خود به آسانی در محیط ویندوز می باشید . صفحه نمایش واضح و قابل تغییر , نمایش راحل حل برای شما , توانایی Load و Save , ویژگی خروجی با فرمت Excell و مجهز به بخشی برای تبدیل واحد های گوناگون به یکدیگر می باشد ( واحد های طولی , وزنی , حجمی , ریالی و ...) .

سایر ویژگی های این نرم افزار شامل  built-in formula interpreter, sales tax functions, cache (memory function), percentage calculation, currency-conversion, floating point- and fixed point-calculation, subdivision into thousands, fast correction key, display of the results in task strip and window title line, printing with heading and date/time, Excel-export و ... می باشد .

ویژگی های کاملتر ....

نسخه ی کامل نرم افزار DeskCalc 3.4.0 با حجم حدود 1.4 مگابایت